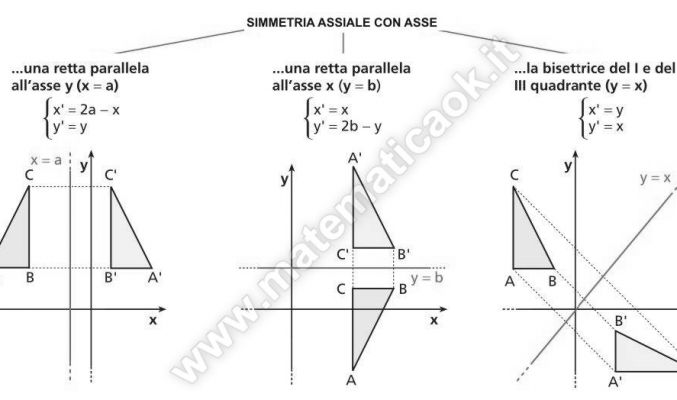
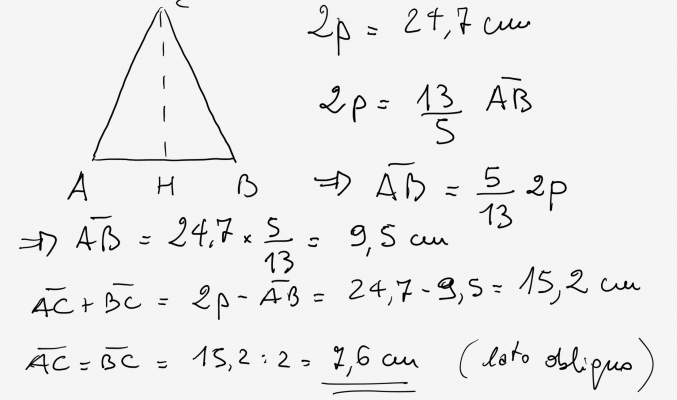Trasformazioni geometriche: glissosimmetria
La glissosimmetria è la composizione di una simmetria assiale con una traslazione di vettore parallelo all’asse della simmetria.
Trasformazioni geometriche: simmetria assiale
Trasformazioni geometriche: simmetria centrale
Trasformazioni geometriche: rotazione
Trasformazioni geometriche: traslazione
Esercizio 57 – Triangolo isoscele – richiesto online da Annamaria
In un triangolo isoscele il perimetro è 24,7 cm ed e i 13/5 della base. Quanto misura un lato obliquo?
Trasformazioni geometriche: retta unita
Data la trasformazione . Trasformiamo la retta generica r: y = mx + q, siccome dobbiamo sostituire le variabili x e y consideriamo l’inversa . Allora da cui ; e quindi la trasformata diventa: Poiché t(r)=r le due rette devono coincidere: per m=1 che è una retta di punti uniti –> y = x – 2 per m=-1 sono unite tutte quelle rette parallele avente coefficiente…
Trasformazioni geometriche: retta di punti uniti
Si definisce retta di punti uniti, quella retta r che ha tutti i suoi punti uniti rispetto alla trasformazione t. , da cui , come si vede otteniamo due rette coincidenti, pertanto la retta y = x – 2 è una retta di punti uniti. In generale, data una trasformazione t e data una curva C, tale trasformazione t trasformerà i punti P della curva C in punti P’ appartenenti…
Trasformazioni geometriche: punti uniti
Per trovare i punti uniti pongo x’ = x ed y’ = y e risolvo il sistema. ESEMPIO Data la trasformazione si ha che da cui , da cui il punto P(1,2) è il punto unito di t. E’ possibile che una trasformazione t possa non avere punti uniti… Ecco un esempio. , da cui tale sistema ovviamente è assurdo e quindi non da soluzioni. E’ possibile che una trasformazione…