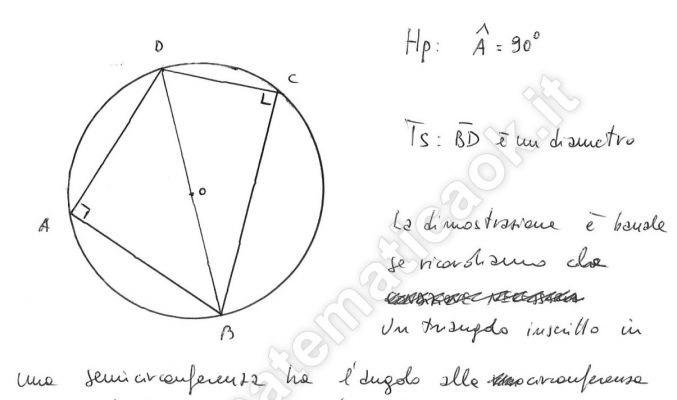
Dimostra che se un quadrilatero inscritto in una circonferenza ha un angolo retto, allora il centro della circonferenza appartiene a una diagonale del quadrilatero.
quadrilatero
Esercizio 65 – Triangolo e quadrilatero inscritto – richiesto online da Guglielmo
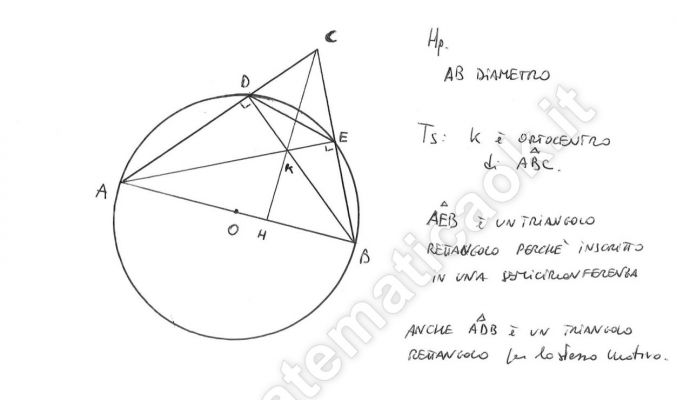
Considera il triangolo ABC con il lato AB coincidente con un diametro di una circonferenza e il vertice C esterno ad essa. Detti D ed E i punti di intersezione della circonferenza con i lati AC e BC, dimostrare che il punto di incontro delle diagonali del quadrilatero inscritto ABED coincide con l’ortocentro del triangolo ABC.
Quadrilatero circoscrittibile ad un cerchio
Un quadrilatero convesso è circoscrittibile ad un cerchio se e solo se la somma delle due coppie di lati opposti è uguale: AB + CD = AD + BC
Quadrilatero inscrittibile in un cerchio
Un quadrilatero convesso è inscrittibile in un cerchio se e solo se gli angoli opposti sono supplementari, ossia