Month: Febbraio 2017

Fra tutti i recipienti a forma cilindrica di uguale superficie S, determina quello di volume massimo.

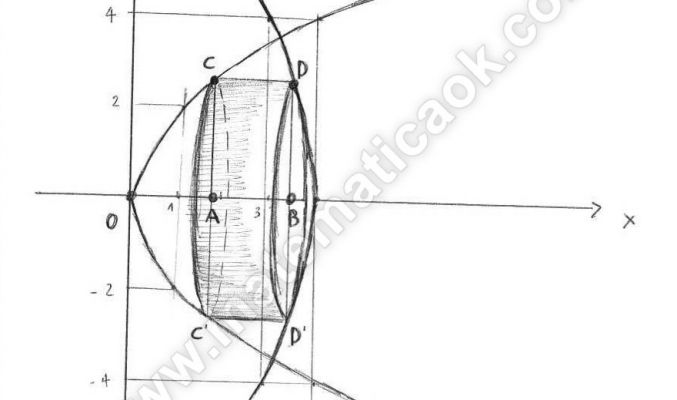
Date le parabole di equazioni  y2 = x  e  y2 = – 16 x – 64  nella zona finita di piano delimitata dalle due parabole inscrivi un rettangolo con i lati paralleli agli assi. Calcola l’altezza del rettangolo in modo che abbia volume massimo il cilindro ottenuto dalla rotazione completa del rettangolo intorno all’asse x.

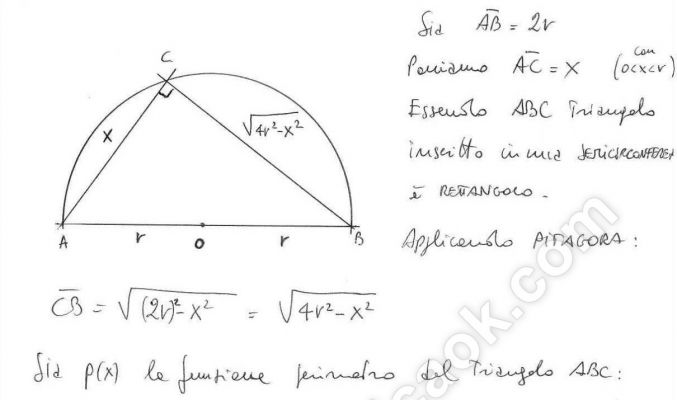
Fra tutti i triangoli inscritti in una semicirconferenza trova quello di perimetro massimo.

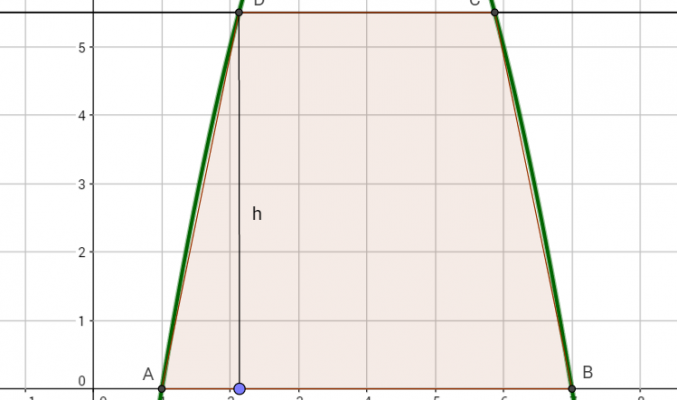
Data la parabola  y = –x2 + 8x – 7,  inscrivi nella parte di piano limitata dalla parabola e dall’asse x un trapezio isoscele con la base maggiore sull’asse x e di area massima.  

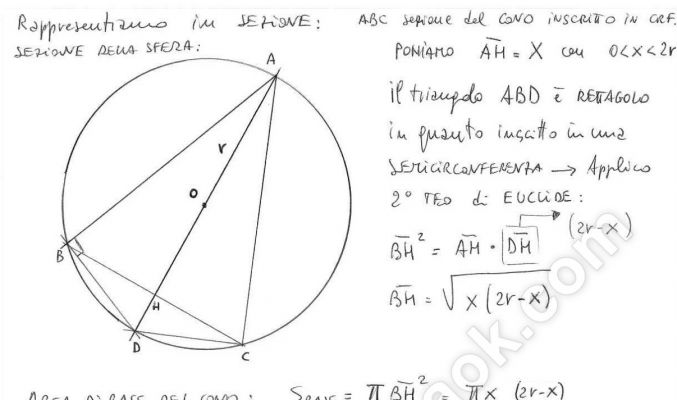
Fra tutti i coni inscritti in una sfera di raggio che misura r, determina quello per il quale è massimo il rapporto tra il suo volume e quello della sfera.

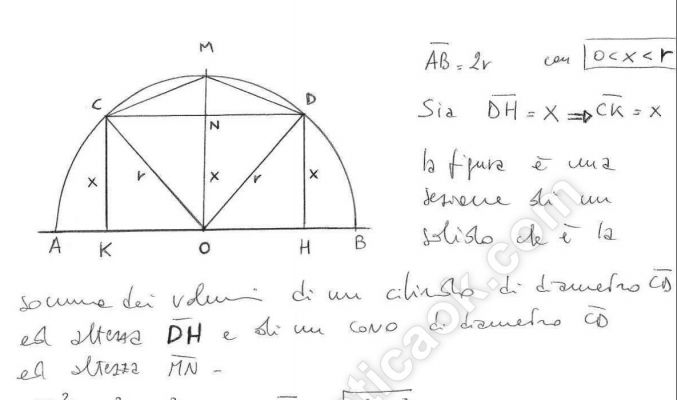
Data una semicirconferenza di diametro AB=2r, sia CD una corda parallela ad AB e siano K e H le proiezioni di C e D sul diametro. Determina la posizione di CD in modo che il solido generato dalla rotazione di CMDHK attorno all’asse di DC abbia volume massimo, con M punto medio dell’arco CD.

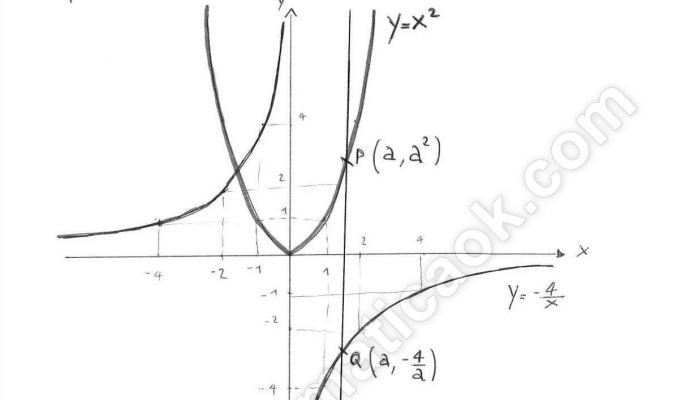
Date la parabola di equazione  y = x2  e l’iperbole equilatera di equazione  xy = –4  considera sulle due curve due punti P e Q con la stessa ascissa a>0. Trova per quale valore di a la distanza PQ è minima.  

In una semicirconferenza di diametro  AB = 2r, conduci una corda AD e sia C il punto medio dell’arco BD. Determina l’angolo BÂC in modo che l’area del quadrilatero ABCD risulti massima.

Fra tutti i triangoli rettangoli ABC di data ipotenusa AB = a, determina quello che genera, in una rotazione completa intorno al cateto AC, un cono di volume massimo.

Fra tutti i rettangoli inscritti nella circonferenza di equazione x2 + y2 = 4, determinare quello di area massima.