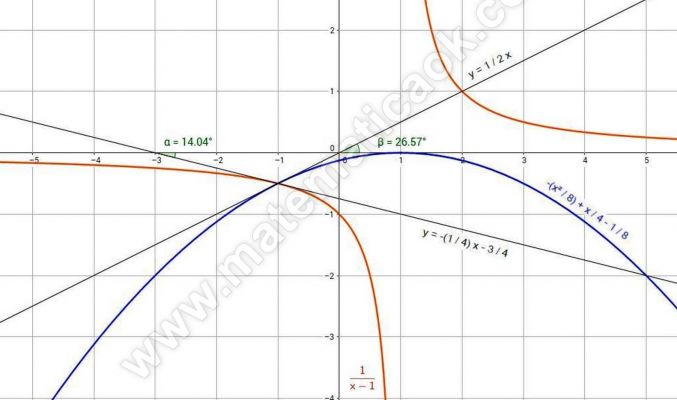
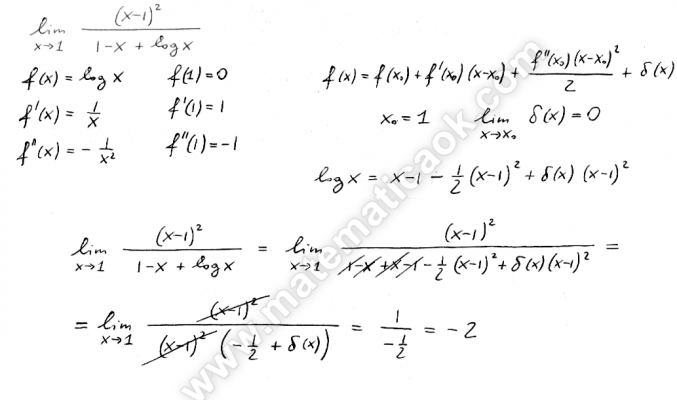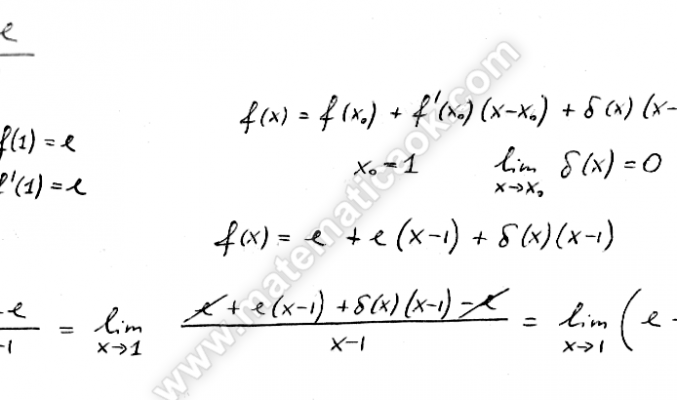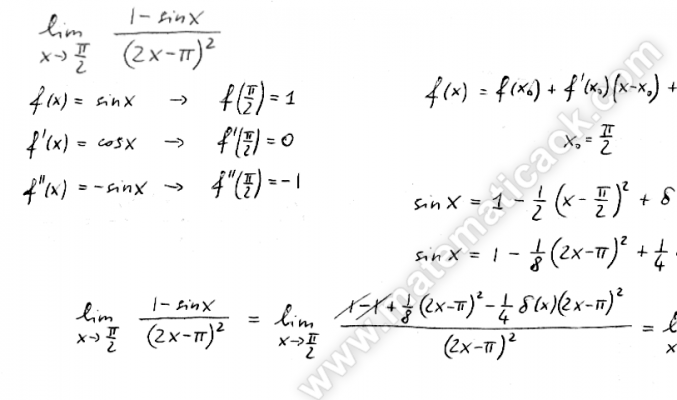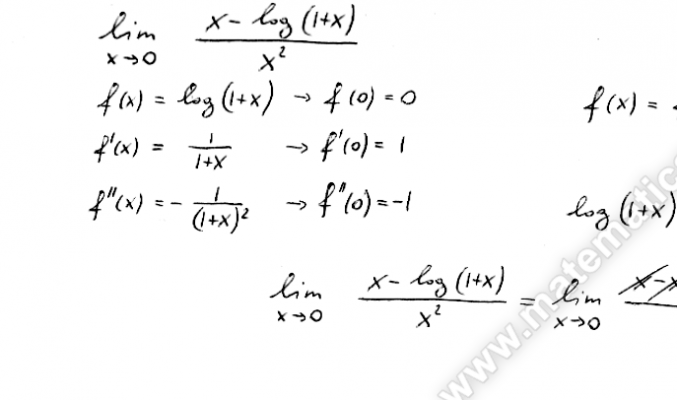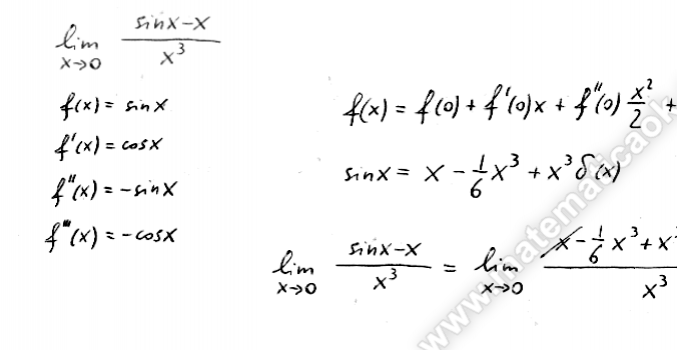Determina l’angolo formato dalle due curve di equazione y = 1 / (x-1) e y = -x2/8 +x/4 – 1/8
Month: Novembre 2016
Esercizio 10 – Ellisse riferita al centro degli assi
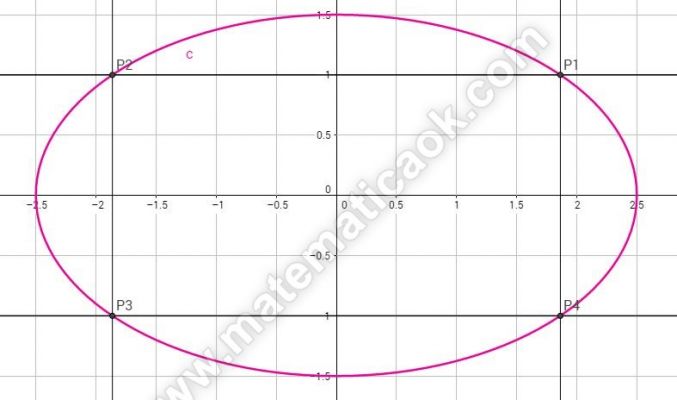
Nell’equazione (a2 – 4) x2 + a2 y2 = a4 – 4a2, si trovi il valore di a2 in modo che l’equazione rappresenti un’ellisse passante per il punto P ( – 5/8 ; 3/8 ). Determinare poi la misura S dell’area del rettangolo, inscritto in tale ellisse, avente un lato appartenente alla retta di equazione y = l .
Esercizio 9 – Ellisse riferita al centro degli assi
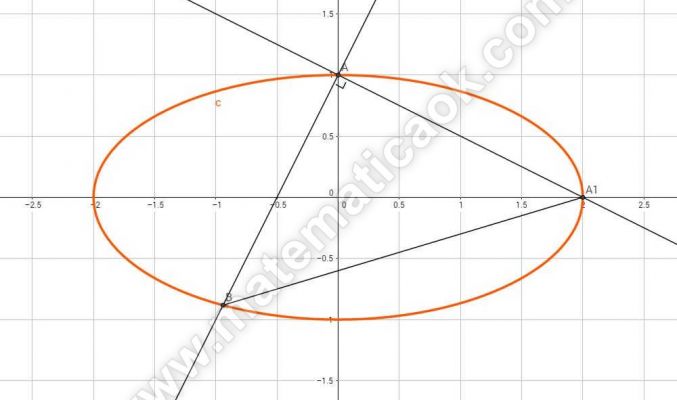
Siano A e B i punti di intersezione dell ellisse di equazione x2 + 4y2 = 4 con la retta di equazione y = 2x + l. Detto A1 il vertice dell’ellisse di ascissa positiva, calcolare la misura dell’area del triangolo ABA1.
Esercizio 3 – Formula di Taylor con il resto di Peano
Scrivere la formula di Taylor di ordine opportuno relativa al punto x0 = 1 e calcolare il seguente limite:
Esercizio 2 – Formula di Taylor con il resto di Peano
Scrivere la formula di Taylor di ordine opportuno relativa al punto x0 = 1 e calcolare il seguente limite:
Esercizio 1 – Formula di Taylor con il resto di Peano
Scrivere la formula di Taylor di ordine opportuno relativa al punto x0 = /2 e calcolare il seguente limite:
Esercizio 4 – Formula di Mac-Laurin con il resto di Peano
Utilizzare la formula di Mac-Laurin di ordine opportuno per calcolare il seguente limite:
Esercizio 3 – Formula di Mac-Laurin con il resto di Peano
Utilizzare la formula di Mac-Laurin di ordine opportuno per calcolare il seguente limite:
Esercizio 2 – Formula di Mac-Laurin con il resto di Peano
Scrivere la formula di Mac-Laurin di secondo ordine della funzione sen x + cos x e calcolare il seguente limite:
Esercizio 1 – Formula di Mac-Laurin con il resto di Peano
Scrivere la formula di Mac-Laurin di terzo ordine della funzione sen x e calcolare il seguente limite: