problemi di massimo

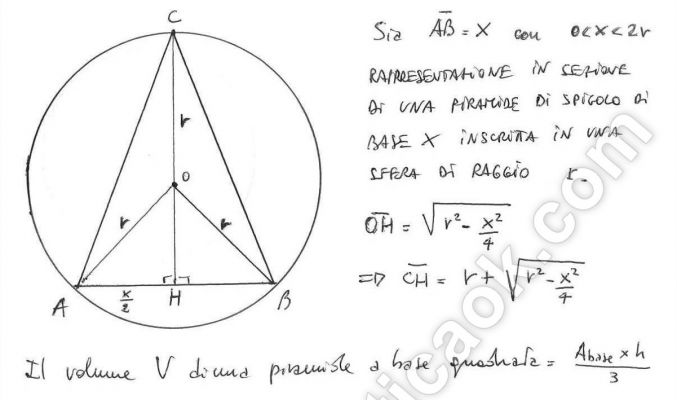
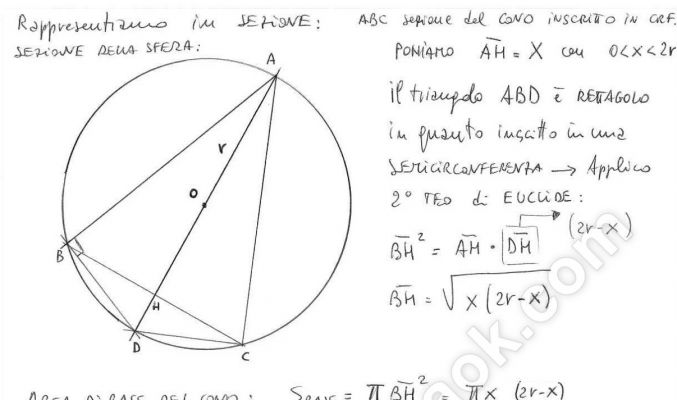
Fra tutte le piramidi regolari a base quadrata inscritte in una sfera di raggio r determina quella che ha il massimo volume.

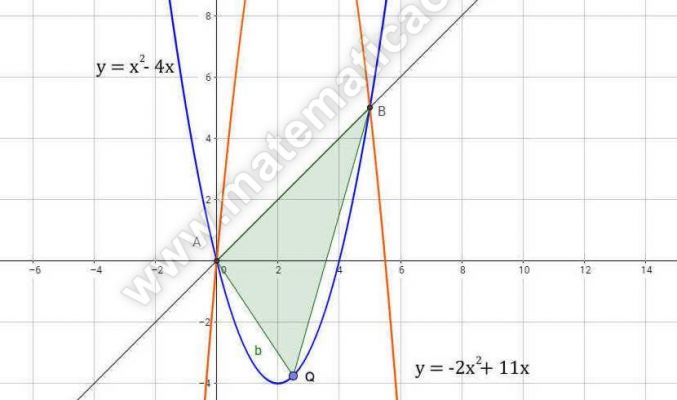
Dopo aver determinato le coordinate dei punti base A e B del fascio di parabole y(a+1) + 2ax² – x(11a+1) = 0, scrivi l’equazione della parabola p del fascio che ha per asse la retta x=2. Nel segmento parabolico delimitato da p e dalla retta AB inscrivi poi il triangolo ABQ di area massima.

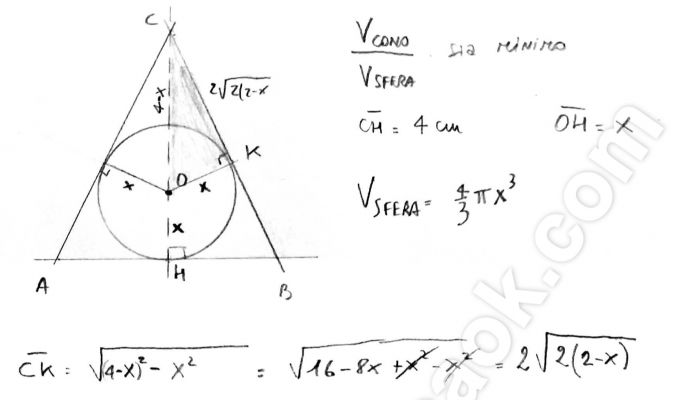
Un cono è generato dalla rotazione completa di un triangolo isoscele ABC, di base AB, intorno alla sua altezza CH.  Sapendo che CH = 4 cm, determina la base AB in modo che sia minimo il rapporto fra il volume del cono e quello della sfera, di centro O, inscritta nel cono.

Individua due numeri la cui somma è 20 e per i quali la somma dei quadrati è minima.

Per una scenografia teatrale si deve preparare una colonna costituita da un cilindro sormontato da una semisfera con la base coincidente con quella del cilindro. Quali devono essere le dimensioni della colonna se si sa che la sua superficie è di 147   dm2  e che il volume deve essere il più grande possibile?

Fra tutti i recipienti a forma cilindrica di uguale superficie S, determina quello di volume massimo.

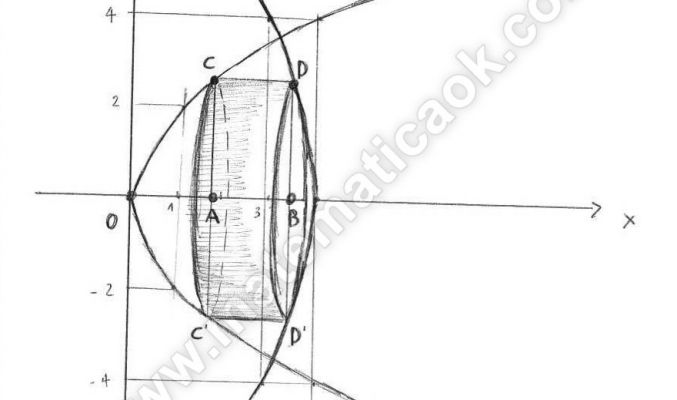
Date le parabole di equazioni  y2 = x  e  y2 = – 16 x – 64  nella zona finita di piano delimitata dalle due parabole inscrivi un rettangolo con i lati paralleli agli assi. Calcola l’altezza del rettangolo in modo che abbia volume massimo il cilindro ottenuto dalla rotazione completa del rettangolo intorno all’asse x.

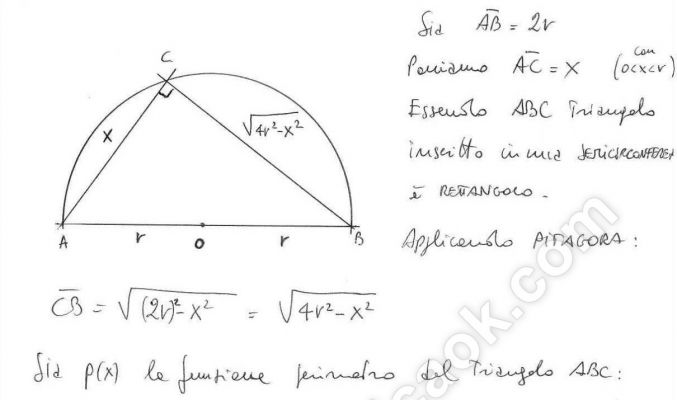
Fra tutti i triangoli inscritti in una semicirconferenza trova quello di perimetro massimo.

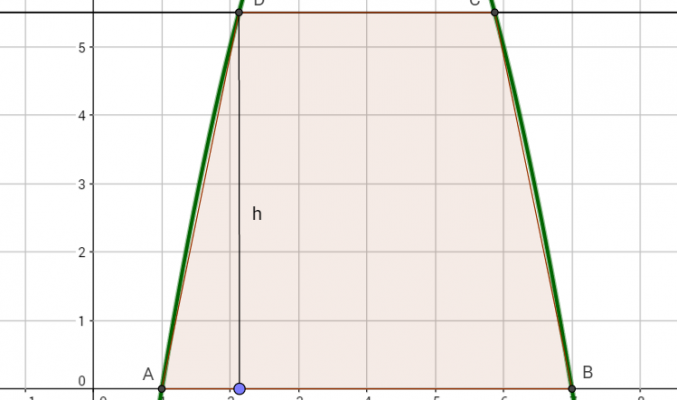
Data la parabola  y = –x2 + 8x – 7,  inscrivi nella parte di piano limitata dalla parabola e dall’asse x un trapezio isoscele con la base maggiore sull’asse x e di area massima.  

Fra tutti i coni inscritti in una sfera di raggio che misura r, determina quello per il quale è massimo il rapporto tra il suo volume e quello della sfera.