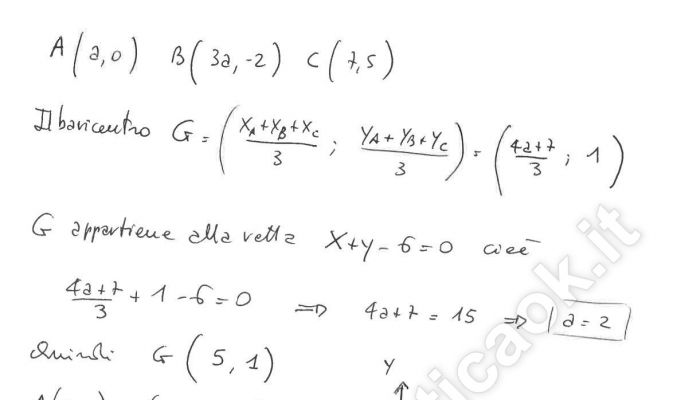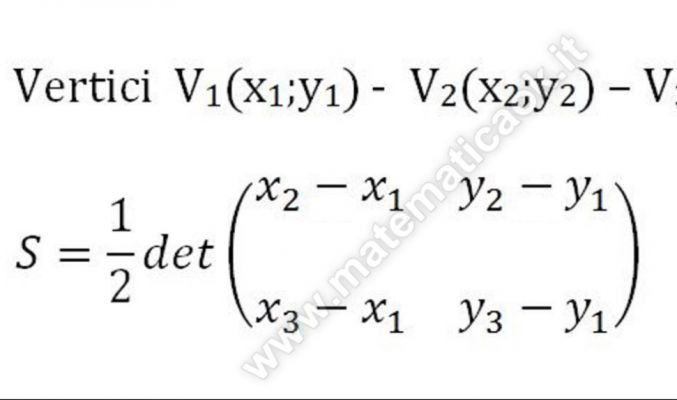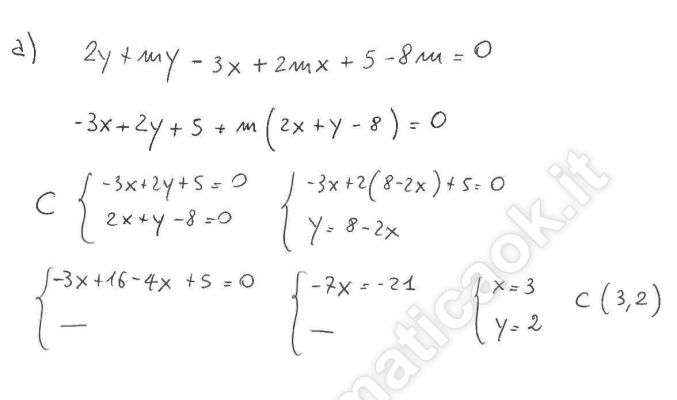… soluzione ai tuoi problemi …
Dopo aver calcolato le coordinate del centro del fascio di rette di equazione (l + k) x + (2 – k) y – 4 – k = 0, determinare per quali valori di k la retta del fascio: 1) è perpendicolare alla retta x + 5y — 3 = 0; 2) passa per il punto di intersezione delle rette x + 3y-5 = 0 e 2x-y + 4 = 0.
Nel triangolo di vertici A(a ; 0), B(3a ; -2), C(7 ; 5) il baricentro appartiene alla retta x + y – 6 = 0. Verificare che il triangolo è isoscele e che la distanza tra il baricentro e il circocentro è 1/6 della base AB.
È dato il fascio di rette di equazione (k – 1) x + (k + 1) y + 2 – k = 0 a) Calcolare le coordinate del centro C del fascio; b) verificare che la retta r del fascio perpendicolare alla retta t di equazione 3x – y = 0 passi per l’origine O del sistema di riferimento; c) calcolare le coordinate dei punti A e B in cui la…
Dati i fasci di rette di equazione: y = h (x – 7) + 4 e y = k (x + 1) – 2 determinare: a) l’equazione della retta comune ai due fasci; b) i valori di h e k affinchè le rette dei due fasci si intersechino perpendicolarmente nei punti P1 e P2 dell’asse y; c) detti C1 e C2 i centri dei fasci, la…
Dato il fascio di rette: (3 – k) x + (1 + 2k) y – 10 + k = 0 Determinare la retta spassante per l’origine O e la retta r ad essa perpendicolare. Determinare poi le coordinate dei vertici del Rombo AOBD aventi due vertici consecutivi rispettivamente in 0 e nel punto A d’intersezione di r con l’asse y ed avente per diagonali r ed s. Determinare la misura…
Dato il fascio di rette di equazione: (2 + m) y – (3 – 2m) x + 5 – 8m = 0; determinare: a) le coordinate del centro C del fascio; b) la retta del fascio avente in comune con la retta r di equazione 9y+5x-86=0 il punto A di ascissa 10; c) la retta del fascio perpendicolare a CA ed il suo punto B d’intersezione con la retta r; d)…
