Per calcolare il raggio della circonferenza inscritta in un triangolo qualsiasi occorre conoscere il perimetro e l’area del triangolo. r = 2 × AREA / PERIMETRO r = AREA / semi PERIMETRO
Sezione aurea o rapporto aureo
La sezione aurea, o rapporto aureo, è il nome che viene dato ad una particolare costante matematica chiamata ϕ = 1,6180339887… (numero irrazionale) Per secoli, questo numero ha affascinato e influenzato generazioni di matematici, pittori, architetti, artisti in genere. Alcuni esempi: – il Partenone, le cui dimensioni seguono le proporzioni del rettangolo aureo; – svariati dipinti di Leonardo da Vinci, tra cui la “Gioconda”, la “Venere della Roccia” e “L’Ultima Cena”, sono stati…
Cubo: definizione, formule e proprietà
Il cubo è un prisma retto con base quadrata e altezza pari allo spigolo di base. E’ costituito da: 8 vertici; 12 spigoli tutti congruenti tra loro; 6 facce tutte congruenti tra loro. FORMULE PRINCIPALI d = l × √3 Abase = l2 Slat = 4 × l2 Stot = 6 × l2 V = l3
Poligoni regolari: definizione, formule e proprietà
Un poligono con n lati è detto regolare se tutti i suoi angoli interni e tutti i suoi lati sono congruenti. Indichiamo con l la misura del lato e con a l’apotema quale segmento perpendicolare a un lato del poligono e che ha come estremo il centro del poligono stesso. Il rapporto a / l = f è chiamato numero fisso del poligono regolare POLIGONO REGOLARE n lati f numero fisso Triangolo 3 0,289 Quadrato 4 0,500…
Esercizio 29 – Trapezio rettangolo – richiesto online da Emma
Un trapezio rettangolo, con l’area di 216 cm2, ha la base minore e l’altezza congruenti. Calcolala misura delle sue basi sapendo che la base maggiore è il doppio della base maggiore.
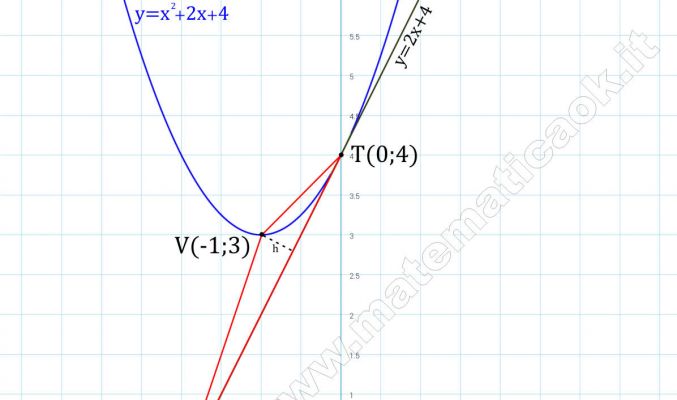
Esercizio 8 – Parabola e retta – richiesto online da Sabrina
Trova la retta tangente alla parabola di equazione y = x2 + 2x + 4 parallela alla retta dì equazione y – 2x = 0. Indicati con T il punto di tangenza, con V il vertice della parabola e con A il punto d’incontro della retta tangente con l’asse delle x, calcola l’area del triangolo AVT.
Quadrato: definizione, formule e proprietà
Un quadrato è un parallelogramma che abbia tutti gli angoli interni congruenti e tutti i lati congruenti. Dalla definizione ne consegue che un quadrato è contemporaneamente un rettangolo e un rombo. Inoltre, essendo equiangolo è un poligono regolare. Un parallelogramma è un quadrato se e solo se le sue diagonali sono congruenti e perpendicolari tra loro, oppure se le diagonali sono congruenti e sono anche bisettrici degli angoli interni. AREA = l…
Rombo: definizione, formule e proprietà
Un rombo è un parallelogramma che ha tutti i lati congruenti fra loro. Un parallelogramma è un rombo se e solo se le sue diagonali sono perpendicolari, o se le diagonali sono anche le bisettrici degli angoli interni. AREA = (AC × BD) / 2 PERIMETRO = 4 × AB
Trapezio: definizione, formule e proprietà
Si chiama trapezio un quadrilatero avente due lati paralleli. I due lati paralleli si dicono basi del trapezio: se non sono congruenti, B la base maggiore e b la base minore. I rimanenti due lati sono i lati obliqui del trapezio; la distanza tra le basi è detta altezza h del trapezio. d1 e d2 sono le diagonali. Proprietà del trapezio isoscele: Gli angoli alle basi sono uguali Le diagonali sono uguali Il lato obliquo di un trapezio…
Rettangolo: definizione, formule e proprietà
Un rettangolo è un parallelogramma che ha tutti gli angoli interni congruenti (cioè di 90° ciascuno). Un parallelogramma è un rettangolo se e solo se ha le diagonali congruenti (cioè AC = BD), o se ha almeno un angolo retto. AREA = AB × BC PERIMETRO = (AB + BC) × 2