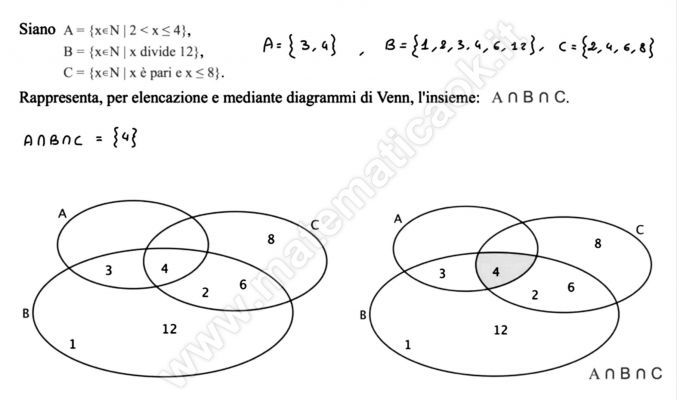
Esercizio 5 – Rappresentazione con diagrammi di Venn
Esercizio 4 – Rappresentazione per elencazione e diagrammi di Venn
Esercizio 3 – Rappresentazione per elencazione e diagrammi di Venn
Esercizio 2 – Rappresentazione per elencazione e diagrammi di Venn
Esercizio 1 – Rappresentazione per elencazione e diagrammi di Venn
Operazioni sugli insiemi: PRODOTTO CARTESIANO
Dati due insiemi A e B non vuoti, definiamo prodotto cartesiano di A e B (nell’ordine) l’insieme delle coppie ordinate (a,b) con a∈A e b∈B; cioè A×B = {(a;b) | a∈A e b∈B}
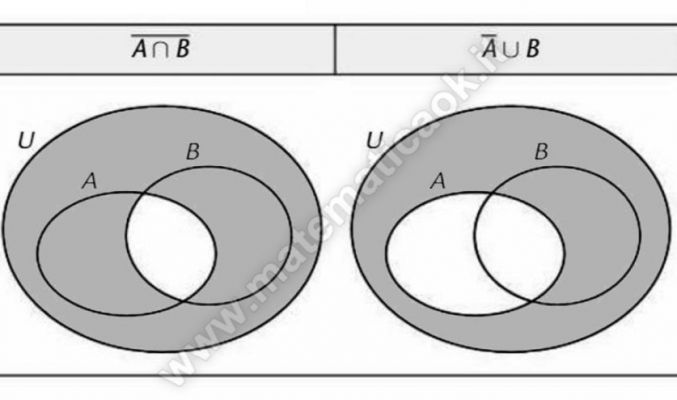
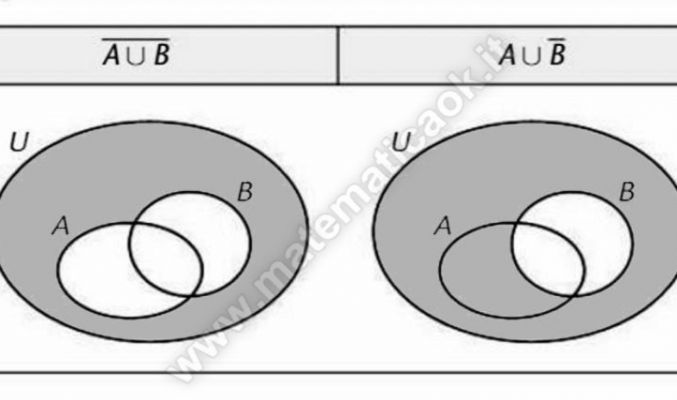
Operazioni sugli insiemi: COMPLEMENTARE
Sia U un insieme qualunque ed A un suo sottoinsieme A ⊆ U. Si dice complementare di A in U e si indica con CU A o anche , l’insieme degli elementi di U che non appartengono ad A
Operazioni sugli insiemi: DIFFERENZA SIMMETRICA
Operazioni sugli insiemi: DIFFERENZA
Dati due insiemi A e B, si dice differenza fra A e B l’insieme formato dagli elementi di A che non appartengono a B e lo denotiamo con A \ B o A – B. Analogamente la differenza fra B ed A è l’insieme formato dagli elementi di B che non appartengono ad A e lo denotiamo con B \ A o B – A. Si deduce che A – B ≠ B – A