Il poliedro ottenuto collegando un punto V nello spazio (detto vertice), non complanare ad un poligono di n lati (base) è detto piramide. L’altezza della piramide è il segmento che congiunge perpendicolarmente il vertice con il piano dove giace la base. Una piramide con base poligonale di n lati ha: n+1 vertici 2n spigoli n+1 facce Una piramide si dice retta se il poligono di base è circoscrittibile a una circonferenza e il “piede”…
Prisma: definizione, formule e proprietà
Un poliedro le cui basi sono due poligoni congruenti di n lati posti su piani paralleli e connessi da una serie di parallelogrammi (dette facce laterali) si chiama PRISMA. Il segmento perpendicolare alle due basi è detto altezza del prisma. Se la base è un triangolo trattasi di prisma triangolare, se la base è un quadrato si tratta di prisma quadrato (o parallelepipedo), se la base è un pentagono abbiamo prisma pentagonale; ecc. Un prisma con base…
Parallelepipedo retto e rettangolo
Un PRISMA qualsiasi che abbia come base un parallelogramma è detto parallelepipedo. Un parallelepipedo retto (detto anche prisma retto a base quadrata) è un poliedro che ha: 4 facce rettangolari e 2 quadrate a due a due congruenti tra loro 12 spigoli 8 vertici Un parallelepipedo rettangolo è un poliedro che ha: 6 facce rettangolari a due a due congruenti tra loro 12 spigoli 8 vertici FORMULE PRINCIPALI Abase = a × b Slat =…
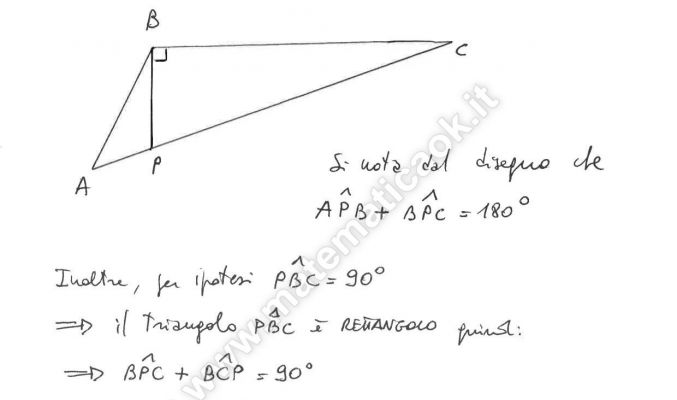
Esercizio 39 – Triangolo ottusangolo – dimostrazione
Nel triangolo ABC, ottusangolo in B, la perpendicolare in B a BC interseca AC nel punto P. Dimostrare che l’angolo APB è il supplementare del complementare dell’angolo in C.
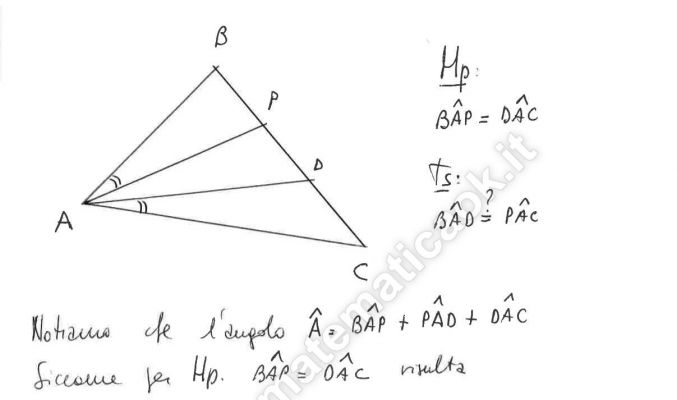
Esercizio 38 – Triangoli qualsiasi – dimostrazione
In un triangolo ABC il punto P del lato BC ed il punto D del segmento PC sono tali che BÂP = DÂC. Dimostrare che BÂD = PÂC.
Esercizio 37 – Quadrato inscritto in un cerchio – richiesto online da Jasmin
Esercizio 18 – Monomi
Esercizio 17 – Monomi
Esercizio 16 – Monomi
