geometria analitica
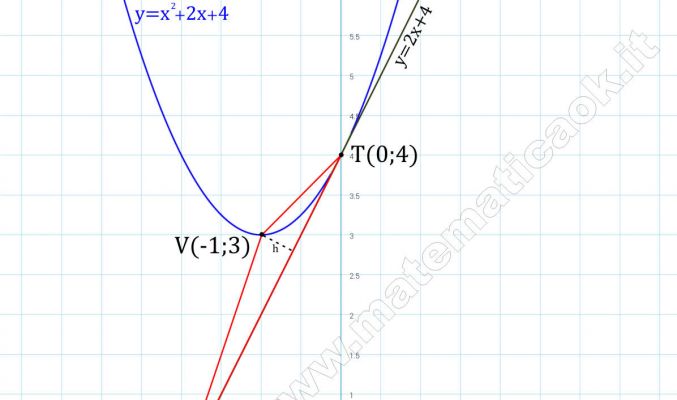
Esercizio 8 – Parabola e retta – richiesto online da Sabrina
Trova la retta tangente alla parabola di equazione y = x2 + 2x + 4 parallela alla retta dì equazione y – 2x = 0. Indicati con T il punto di tangenza, con V il vertice della parabola e con A il punto d’incontro della retta tangente con l’asse delle x, calcola l’area del triangolo AVT.
Esercizio 23 – Circonferenze e rette
Determinare se la retta 2x – y + 1 = 0 è TANGENTE, SECANTE o ESTERNA alla circonferenza di equazione x2 + y2– 2x + 4y = 0
Esercizio 22 – Intersezione di circonferenze
Calcolare la lunghezza della corda comune alle seguenti circonferenze: x2 + y2 – 4x + 8y = 0 e x2 + y2 + 2x – 10y – 24 = 0
Esercizio 21 – Circonferenze e rette
Scrivere l’equazione della circonferenza passante per l’origine O ed avente il centro nel punto comune alle rette: 3x – y + 7 = 0 e x – y + 1 = 0
Esercizio 20 – Circonferenze e punti
Determinare se il punto A(1,-2) è interno, esterno o appartiene alla circonferenza di equazione x2 + y2 -8x -4y -5 = 0
Esercizio 19 – Fascio di circonferenze
Studia il fascio di circonferenze di equazione x2 + y2 – (2 + k) x + (k – 2) y + 2 = 0 indicando le sue caratteristiche. Trova poi la circonferenza del fascio: a) tangente all’asse x; b) che racchiude un’area 8; c) il cui centro appartiene alla retta y = 2x – 5; d) tangente alla retta y = x – 4.
Esercizio 18 – Fascio di circonferenze
Studia il fascio di circonferenze x2 + y2 – 2x + 4y + k(x + y – 20) = 0. Quale circonferenza del fascio ha il centro nell’origine degli assi? Scrivi l’equazione del fascio di circonferenze simmetrico al fascio dato rispetto all’asse x e trova per quali valori di k si hanno nei due fasci le circonferenze con il centro rispettivamente sull’asse y e sull’asse x.
Esercizio 17 – Fascio di circonferenze
Considera il fascio di circonferenze di equazione x2 + y2 + 2x – 4y + k = 0 e studia le sue caratteristiche; trova poi per quali valori di k si ha una circonferenza che: a) ha raggio minimo; b) passa per il punto P(-2; 1); c) ha raggio uguale a 5; d) è tangente alla retta di equazione 2x + y – 1 = 0.
Esercizio 16 – Fascio di circonferenze
Dopo aver studiato il fascio di circonferenze di equazione x2 + y2 – 6x + (k – 2) y + 6 – 2k = 0, trova per quali valori di k si ha una circonferenza: a) di raggio uguale a 2; b) che racchiude un’area uguale a 7; c) con il centro che ha distanza dalla retta di equazione x + 2y – 1 = 0 minore di 2.