Sia f: [a,b] –> R una funzione CONTINUA, allora f(x) assume almeno un massimo ed un minimo assoluti in [a,b]
Month: Novembre 2015
Retta
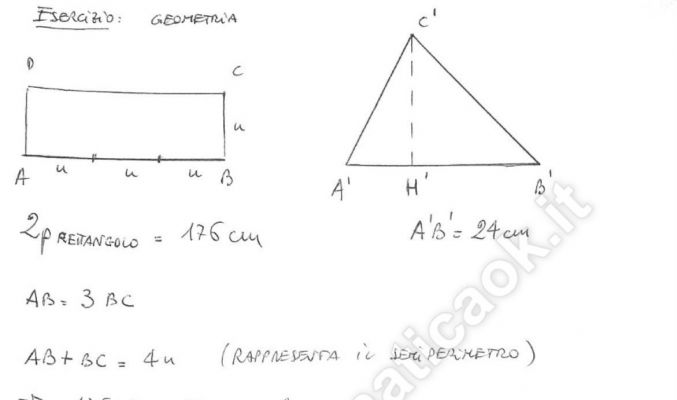
Esercizio 2 – Geometria piana
Intervalli: rappresentazione
Proprietà dei radicali
Teorema di De L’Hôpital
Siano date due funzioni f(x) e g(x), che supponiamo definite e derivabili in tutti i punti di un intorno I del punto c (finito o infinito), escluso al più c stesso. Supponiamo inoltre che che il limite del rapporto delle due funzioni,si presenti in una forma indeterminata del tipo [0 su 0] oppure [infinito su infinito] e sia g'(x)≠0 in tutti i punti di I, escluso al più x = c. In tali ipotesi, se…
Teorema di Cauchy
Siano date y=f(x) e y=g(x) due funzioni continue in un intervallo chiuso e limitato [a,b] e derivabili nei punti interni di tale intervallo (a,b); inoltre g'(x)≠0 in (a,b), allora esiste almeno un punto c di (a,b) tale che
Teorema di Lagrange o del valore medio
Sia y=f(x) una funzione continua in un intervallo chiuso e limitato [a,b] e derivabile nei punti interni di tale intervallo (a,b); se f(a) = f(b), allora esiste almeno un punto Osservazione Si noti che, come si è affermato, esiste almeno un punto in cui la tangente alla curva è parallela alla corda AB, ma ciò non esclude che ve ne sia più di uno, come avviene, in figura.
Teorema di Rolle
Sia y=f(x) una funzione continua in un intervallo chiuso e limitato [a,b] e derivabile nei punti interni di tale intervallo (a,b); se f(a) = f(b), allora esiste almeno un punto c di (a,b) tale che f ‘(c)=0 OSSERVAZIONE: Significato geometrico del Teorema di Rolle: è evidente che se valgono le ipotesi del teorema, esiste almeno un punto interno all’intervallo [a,b] in cui la tangente alla curva è parallela all’asse delle x