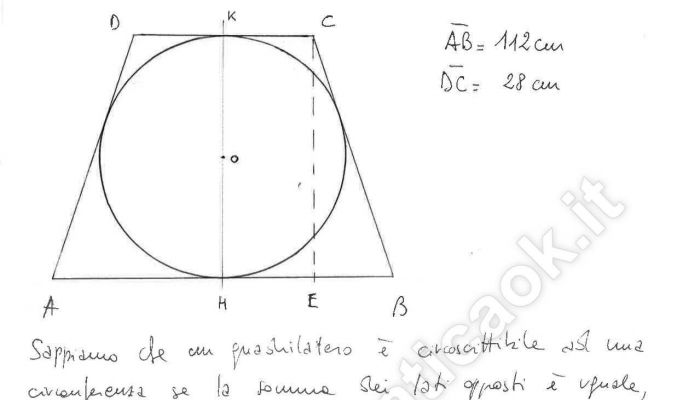
Un trapezio isoscele è circoscritto a una circonferenza. Sapendo che le due basi misurano rispettivamente 112 cm e 28 cm, calcola: a) il perimetro e l’area del trapezio; b) la lunghezza della circonferenza e l’area del cerchio.
cerchio
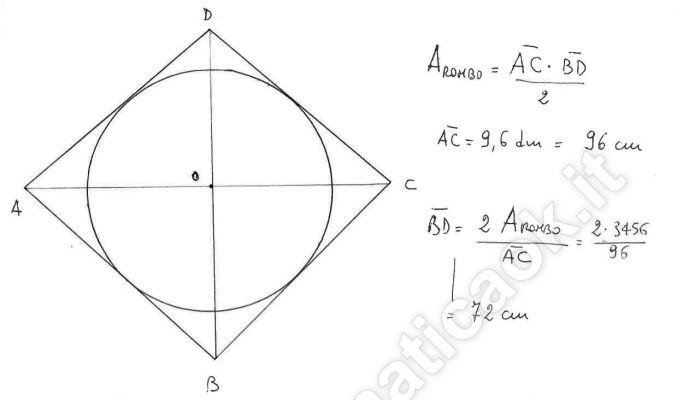
Esercizio 11 – Rombo circoscritto ad una circonferenza
L’area di un rombo circoscritto a una circonferenza è di 3456 cm2 e una sua diagonale misura 9,6 dm. Trovare l’area del cerchio.
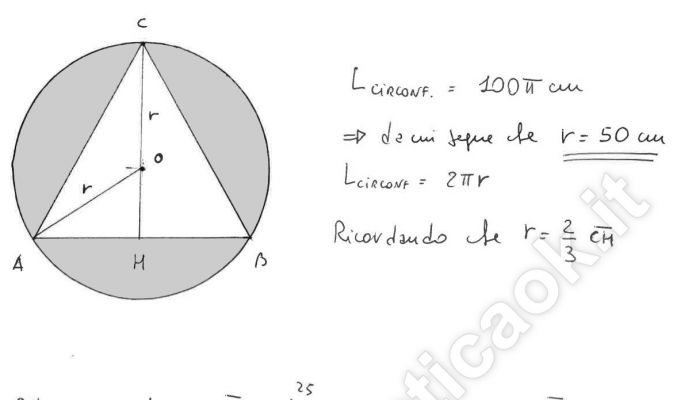
Esercizio 10 – Triangolo equilatero inscritto in circonferenza
Un triangolo equilatero è inscritto in una circonferenza di 100 cm. Calcola: a) l’area del triangolo; b) l’area del cerchio; c) l’area della parte di cerchio colorata.
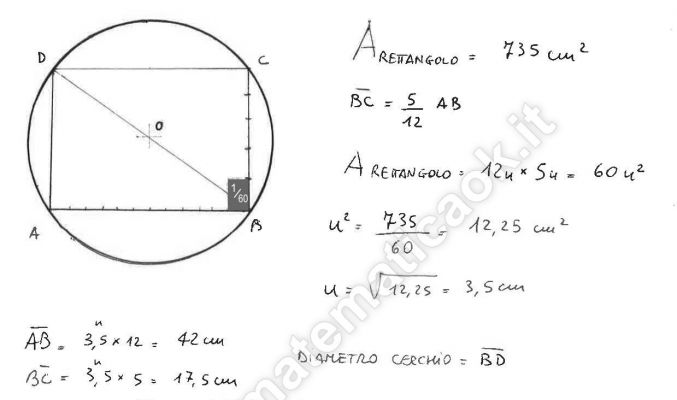
Esercizio 9 – Rettangolo inscritto in circonferenza
Un rettangolo inscritto in una circonferenza ha l’area di 735 cm2 e le sue dimensioni sono una i 5/12 dell’altra. Calcola la lunghezza della circonferenza e l’area del cerchio.
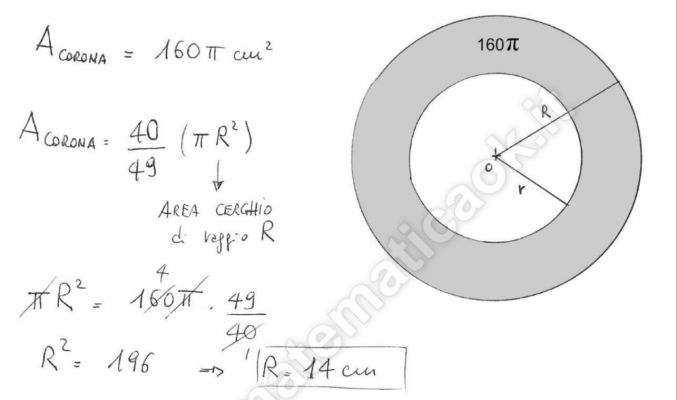
Esercizio 8 – Cerchio, corona circolare
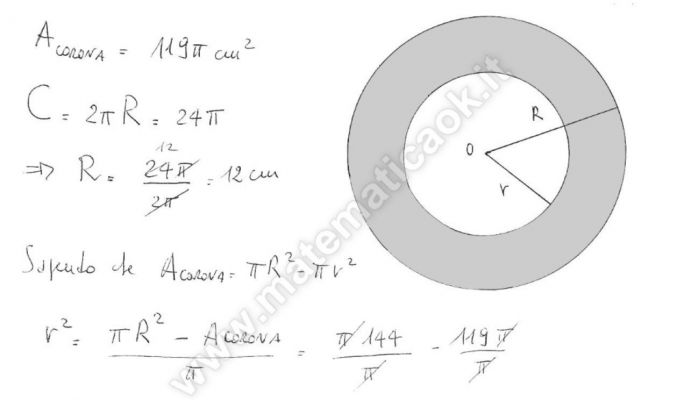
Esercizio 7 – Cerchio, corona circolare
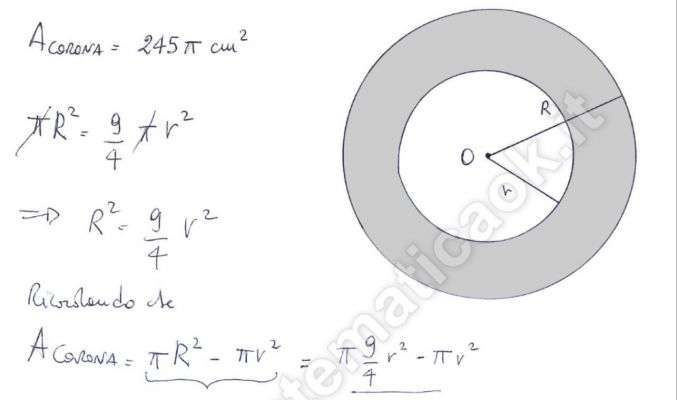
Esercizio 6 – Cerchio, corona circolare
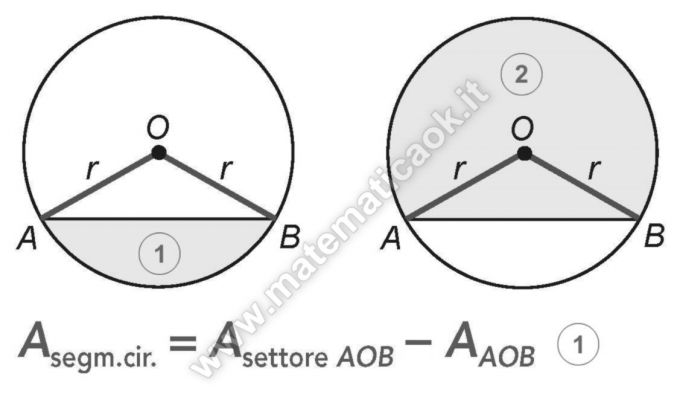
Area del segmento circolare: Teoria
L’area del segmento circolare a una base che non contiene – 1 – (o contiene – 2 -) il centro del cerchio è uguale alla differenza (o alla somma) tra l’area del settore circolare che insiste sul suo stesso arco e l’area del triangolo i cui lati sono due raggi e la corda che sottende l’arco.
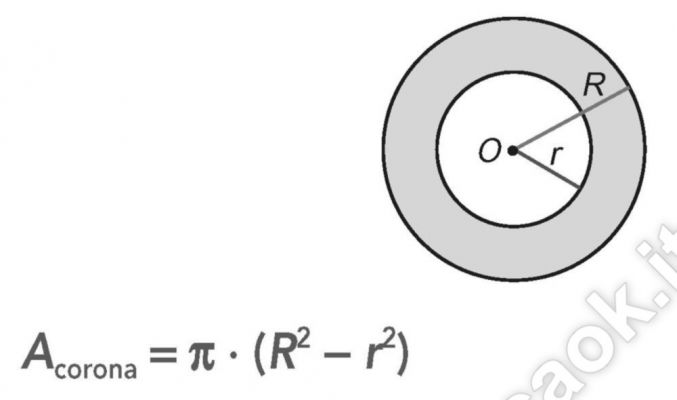
Corona circolare e Settore circolare: Teoria
L’area della corona circolare è uguale alla differenza delle aree dei due cerchi concentrici che la delimitano. L’area del settore circolare è direttamente proporzionale alla sua ampiezza e il cerchio si può considerare il settore di ampiezza massima, cioè di 360°; ovvero l’area del settore circolare è uguale al semiprodotto del raggio e dell’arco corrispondente.