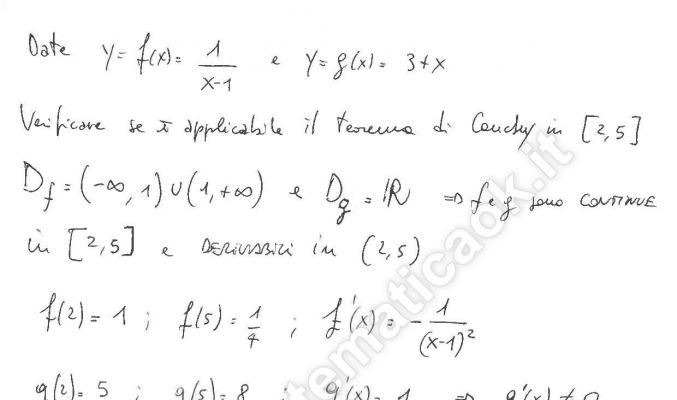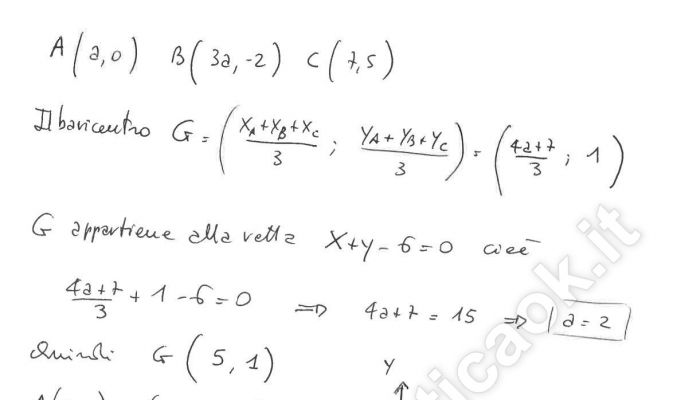esercizi svolti
Esercizio 3 – Teorema di Cauchy: applicazioni
Esercizio 2 – Teorema di Cauchy: applicazioni
Esercizio 19 – Fascio di rette
Dato il fascio di rette di equazione (2 + k) x + (k – 1) y + 3 – k = 0, determinare: 1) le coordinate del centro del fascio; 2) il valore di k per cui vi è una retta del fascio parallela alla retta passante per A (2 ; 1) e per B(0 ; 3) e giustificare il risultato ottenuto; 3) i valori di k per i quali…
Esercizio 18 – Fascio di rette
Dopo aver calcolato le coordinate del centro del fascio di rette di equazione (l + k) x + (2 – k) y – 4 – k = 0, determinare per quali valori di k la retta del fascio: 1) è perpendicolare alla retta x + 5y — 3 = 0; 2) passa per il punto di intersezione delle rette x + 3y-5 = 0 e 2x-y + 4 = 0.
Esercizio 1 – Teorema di Cauchy: applicazioni
Esercizio 17 – Fascio di rette
Nel triangolo di vertici A(a ; 0), B(3a ; -2), C(7 ; 5) il baricentro appartiene alla retta x + y – 6 = 0. Verificare che il triangolo è isoscele e che la distanza tra il baricentro e il circocentro è 1/6 della base AB.
Esercizio 16 – Fascio di rette
È dato il fascio di rette di equazione (k – 1) x + (k + 1) y + 2 – k = 0 a) Calcolare le coordinate del centro C del fascio; b) verificare che la retta r del fascio perpendicolare alla retta t di equazione 3x – y = 0 passi per l’origine O del sistema di riferimento; c) calcolare le coordinate dei punti A e B in cui la…
Esercizio di geometria su angoli supplementari
Due angoli sono supplementari e il secondo angolo supera il doppio del primo di 15°. Calcola l’ampiezza di ciascun angolo.
Esercizio 4 – Calcolo di aree di figure piane
Data la parabola 9y = -4×2 + 24x e la retta y = x che la taglia nei punti A e B, trovare la misura dell’area della parte di piano limitata dalle tangenti in A e in B e dalla curva.