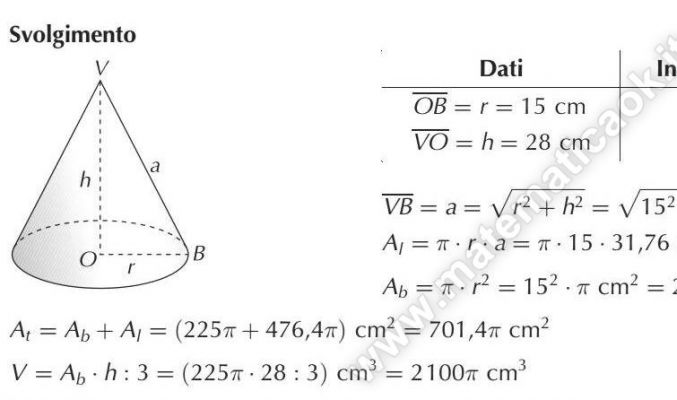
Un cono ha la misura del raggio di base e dell’altezza rispettivamente di 15 cm e 28 cm; calcola l’area della superficie totale ed il volume.
geometria solida
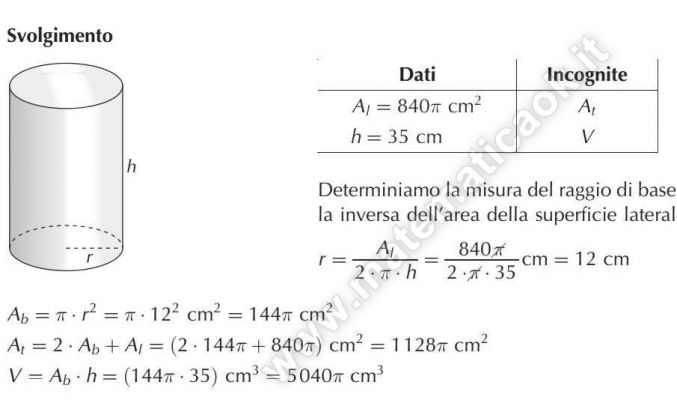
Esercizio 18 – Superficie totale e volume del cilindro
L’area della superficie laterale e la misura dell’altezza di un cilindro sono rispettivamente 840 cm2 e 35 cm; calcola l’area della superficie totale e il volume del cilindro.
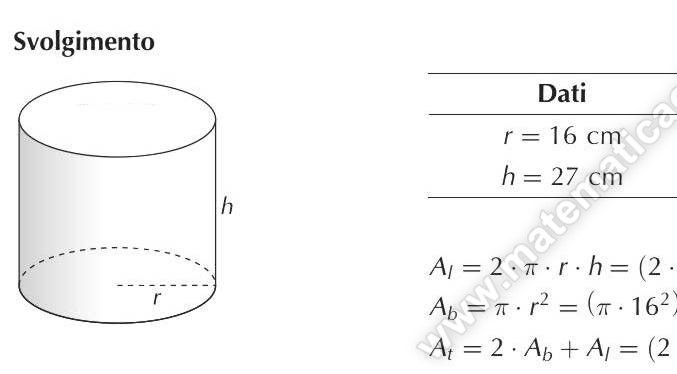
Esercizio 17 – Superficie totale del cilindro
Le misure del raggio di base e dell’altezza di un cilindro sono rispettivamente 16 cm e 27 cm; calcola l’area della superficie totale del cilindro.
Esercizio 16 – Solido composto da due cubi sovrapposti – richiesto online da Martina
Un solido è formato da due cubi sovrapposti i cui spigoli misurano rispettivamente 12 cm e 7 cm. Calcola l’area della superficie totale e il volume del solido composto.
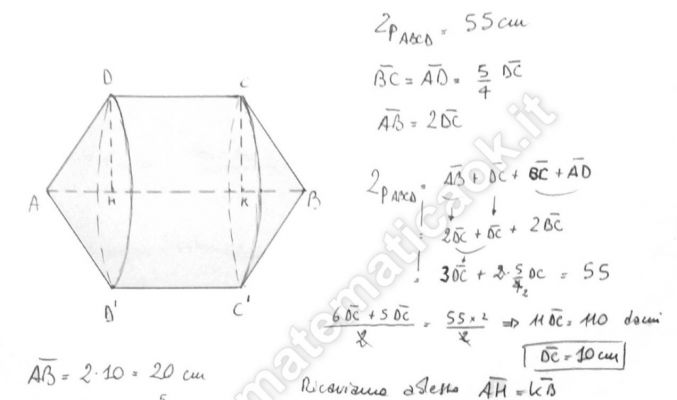
Esercizio 15 – Solido di rotazione da trapezio isoscele – richiesto online da Alessandro
Il trapezio isoscele ha il perimetro di 55 cm,il lato obliquo è i 5/4 della base minore e la base maggiore è il doppio di quella minore. Calcola l’area della superficie totale ed il volume del solido ottenuto facendo ruotare il trapezio attorno alla base maggiore.
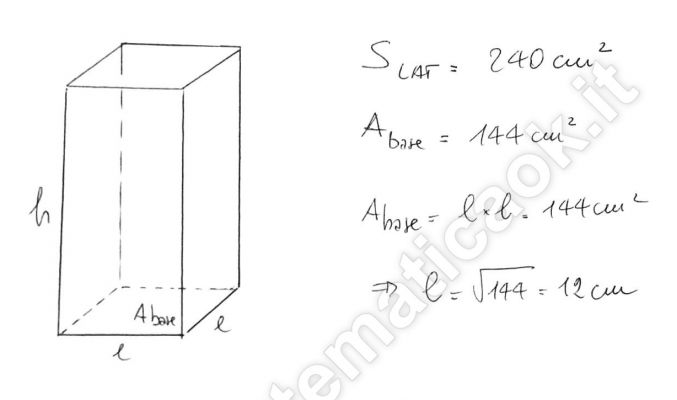
Esercizio 14 – Parallelepipedo a base quadrata – richiesto online da Martina
La superficie laterale di un parallelepipedo a base quadrata è 240 cm2. Calcola la misura dell’altezza sapendo che l’area di base è 144 cm2.
Esercizio 13 – Cono
Un cono ha il diametro di base di 12 cm e l’apotema di 10 cm. Calcola la superficie e il suo volume.
Esercizio 12 – Cono
Un cono ha un volume di 2.560 cm3. Calcola la superficie totale del solido, sapendo che il suo diametro di base è di 32 cm.
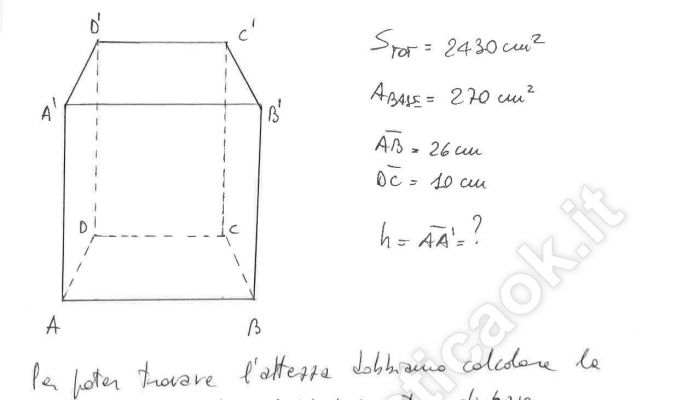
Esercizio 11 – Prisma retto con la base di un trapezio isoscele
L’area della superficie totale di un prisma retto che ha per base un trapezio isoscele è 2.430 cm2 e l’area di base è 270 cm2. Calcola la misura dell’altezza del prisma sapendo che la base maggiore e la base minore del trapezio misurano rispettivamente 26 cm e 10 cm.
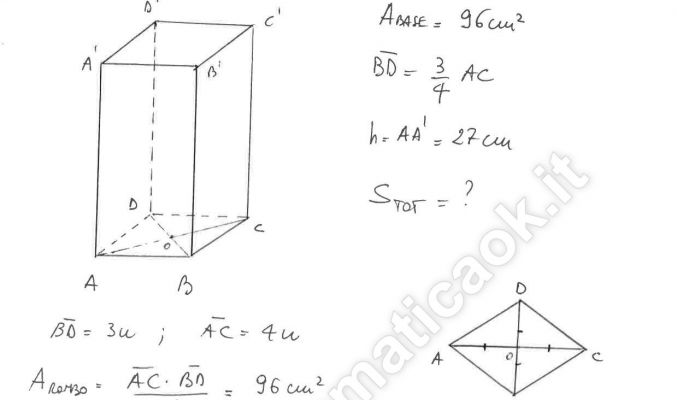
Esercizio 10 – Prisma retto a base rombica
L’area di base di un prisma retto a base rombica è 96 cm2. Determina l’area della superficie totale del prisma sapendo che le diagonali di base sono una i 3/4 dell’altra e che l’altezza misura 27 cm.