… soluzione ai tuoi problemi …
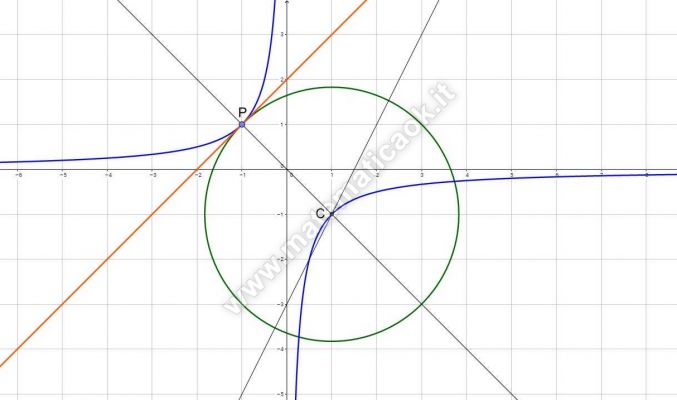
Scrivere l’equazione della circonferenza tangente alla retta y=x+2 nel punto P(-l;l) ed avente centro sulla retta di equazione 2x-y-3=0. Determinare poi l’equazione dell’iperbole equilatera riferita ai propri asintoti che passa per il centro della circonferenza.
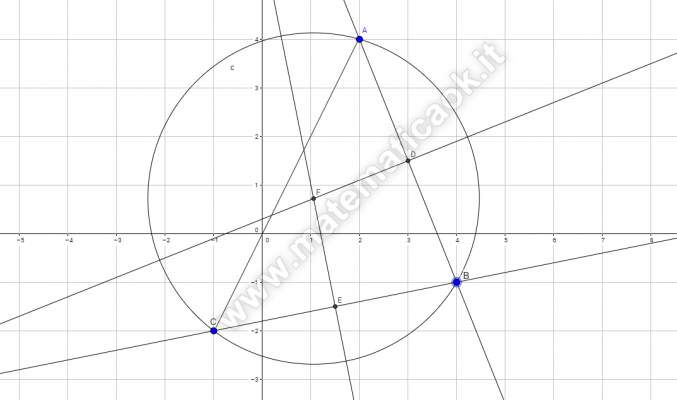
Determina il centro della circonferenza circoscritta al triangolo di vertici A(2;4), B(4; -1), C(-1;-2).
a) Scrivi l’equazione della retta r passante per i punti A(4; 0) e B(0; 6). b) Individua la retta s parallela alla bisettrice del primo e terzo quadrante e passante per il punto C(—1; 0). c) Nel fascio di rette generato da r e da s determina l’equazione della retta t parallela alla retta x — 2y + 5 = 0. d) Sia D l’intersezione della retta del fascio avente coefficiente…
Dal punto P (2 ; 1) si conduca la retta r di coefficiente angolare -2 e la retta s perpendicolare a r. Determinare una parallela all’asse x che intercetti con r ed s un segmento di misura 0,5.
Determinare i punti che sono equidistanti dall’asse x e dalla retta di equazione 3 x – 4 y = 0 e che appartengono al luogo dei punti per i quali la differenza dei quadrati delle distanze da A (2 ; 1) e B (-1; 2) è uguale a 3.
Dato il fascio di rette di equazione (2 + k) x + (k – 1) y + 3 – k = 0, determinare: 1) le coordinate del centro del fascio; 2) il valore di k per cui vi è una retta del fascio parallela alla retta passante per A (2 ; 1) e per B(0 ; 3) e giustificare il risultato ottenuto; 3) i valori di k per i quali…