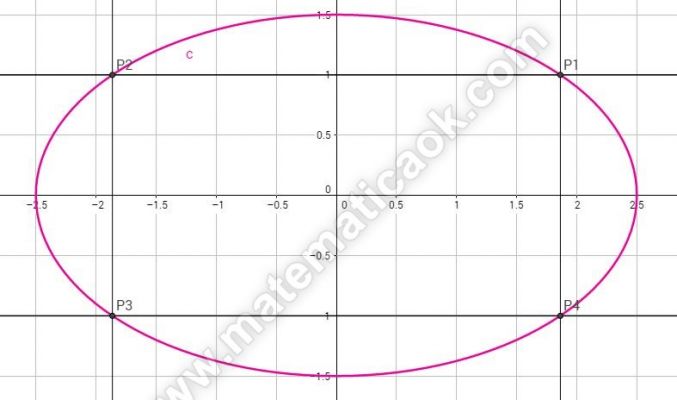
Nell’equazione (a2 – 4) x2 + a2 y2 = a4 – 4a2, si trovi il valore di a2 in modo che l’equazione rappresenti un’ellisse passante per il punto P ( – 5/8 ; 3/8 ). Determinare poi la misura S dell’area del rettangolo, inscritto in tale ellisse, avente un lato appartenente alla retta di equazione y = l .
geometria analitica
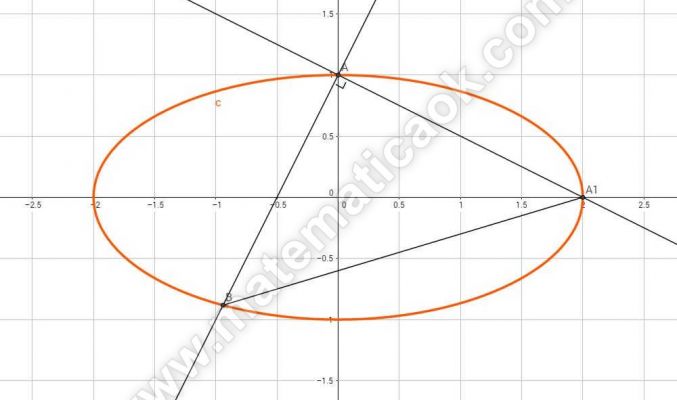
Esercizio 9 – Ellisse riferita al centro degli assi
Siano A e B i punti di intersezione dell ellisse di equazione x2 + 4y2 = 4 con la retta di equazione y = 2x + l. Detto A1 il vertice dell’ellisse di ascissa positiva, calcolare la misura dell’area del triangolo ABA1.
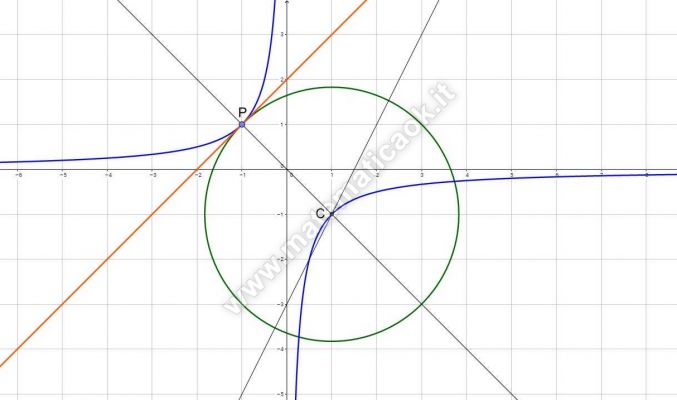
Esercizio 28 – Circonferenza, retta, iperbole equilatera richiesta online da Leonardo
Scrivere l’equazione della circonferenza tangente alla retta y=x+2 nel punto P(-l;l) ed avente centro sulla retta di equazione 2x-y-3=0. Determinare poi l’equazione dell’iperbole equilatera riferita ai propri asintoti che passa per il centro della circonferenza.
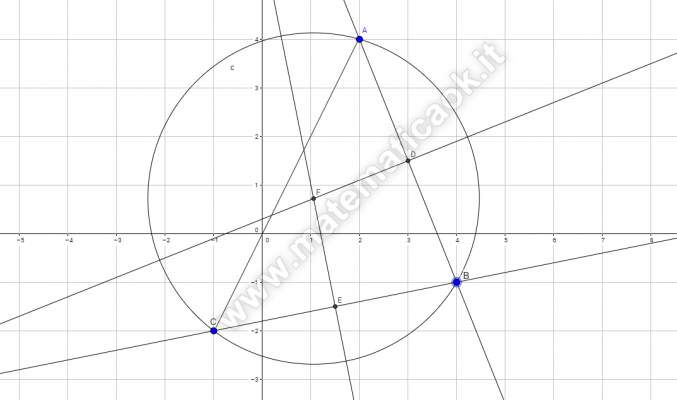
Esercizio 27 – Trovare il Circocentro – richiesto online da Paolo
Determina il centro della circonferenza circoscritta al triangolo di vertici A(2;4), B(4; -1), C(-1;-2).
Esercizio 26 – Fascio di Parabole
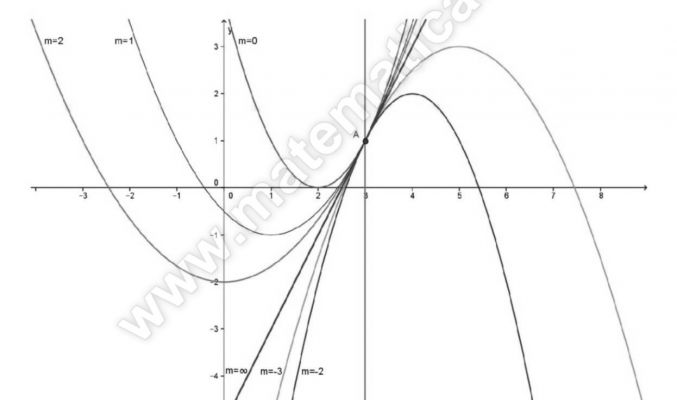
Dato il fascio di parabole di equazione y= k x2 + (3 – 3k) x + 2k – 8 determinarne a) le generatrici; b) i punti base; c) le parabole degeneri. Determinare inoltre per quali valori di k: d) la parabola del fascio che passa per P( 3 ; -1); e) per cui le parabole del fascio hanno il vertice nel primo o nel quarto quadrante.
Esercizio 25 – Parabola, retta tangente e circonferenza
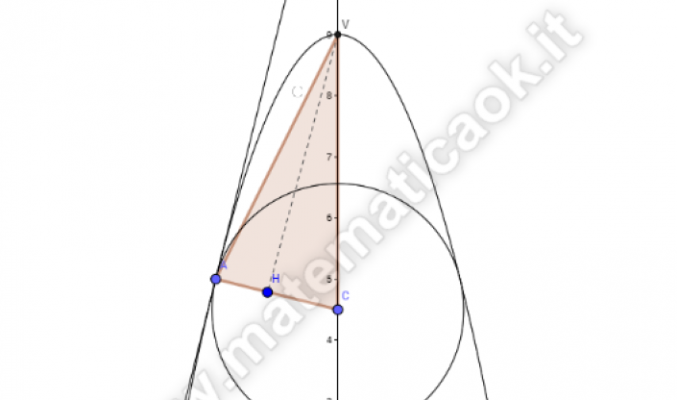
Determina e rappresenta l’equazione della parabola con asse parallelo all’asse y con vertice in V(0; 9) e passante per A ( — 2; 5). Successivamente trova e rappresenta l’equazione della retta t tangente in A alla parabola. Scrivi l’equazione della circonferenza con il centro C sull’asse y e tangente in A alla retta t e rappresentala graficamente. Detto V il vertice della parabola, calcola l’area del triangolo A VC.
Esercizio 24 – Fascio di parabole
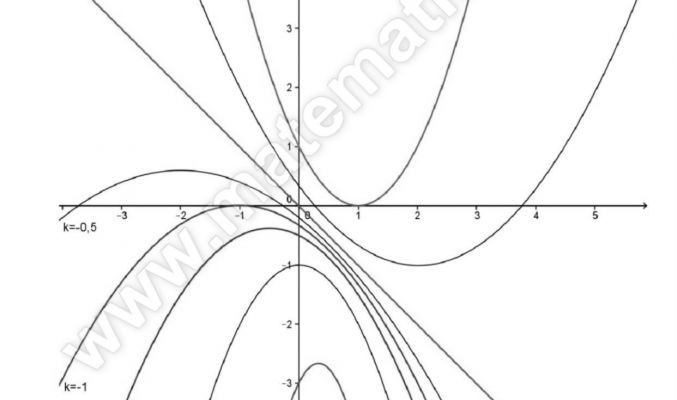
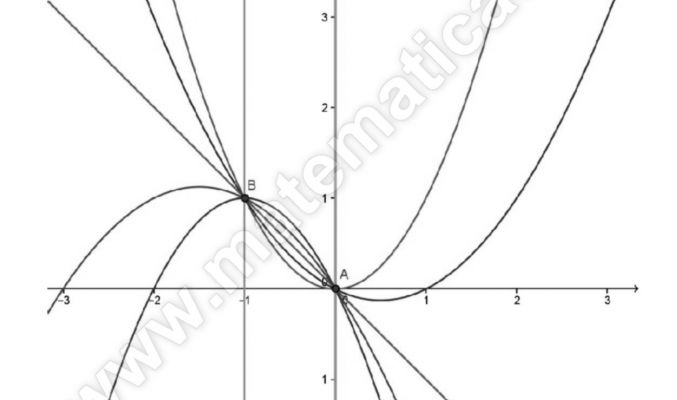
Studia il fascio di parabole di equazione (m + 1) x2 — 4 (m + 1) x — (m + 1) y + 4 + 5m = 0 e determinare poi la parabola del fascio: a) passante per il punto A(3; — 3); b) che intercetta sull’asse delle ascisse un segmento di lunghezza 6; c) tangente alla retta 2x — y — 3 = 0; d) che forma nel I…