… soluzione ai tuoi problemi …
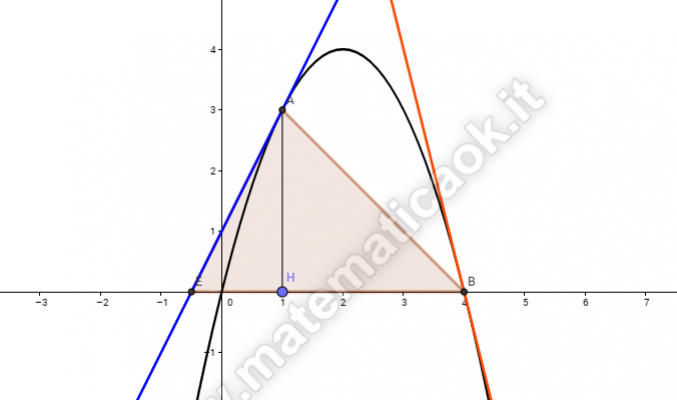
Determina le coordinate dei punti di intersezione, A e B, della parabola y = — x2 + 4x con la retta y = —x + 4 indicando con A il punto di ascissa minore. Conduci dal punto C(5/2;6) le rette tangenti alla parabola e verifica che i punti di tangenza sono A e B. Detto E il punto in cui la tangente in A interseca l’asse x, calcola l’area del triangolo EBC.
Scrivi l’equazione della retta parallela all’asse x sulla quale la circonferenza di equazione x2 + y2 + 2x + 8y = 0 stacca una corda di lunghezza 4√2
a) Scrivi l’equazione della retta r passante per i punti A(4; 0) e B(0; 6). b) Individua la retta s parallela alla bisettrice del primo e terzo quadrante e passante per il punto C(—1; 0). c) Nel fascio di rette generato da r e da s determina l’equazione della retta t parallela alla retta x — 2y + 5 = 0. d) Sia D l’intersezione della retta del fascio avente coefficiente…
Data la parabola y = x2 + bx + 3, trova b in modo che: a) abbia il vertice sull’asse y; b) sia tangente alla bisettrice del II e IV quadrante; c) sia tangente all’asse x; d) stacchi sulla retta y = – 3 una corda lunga 6.
Considera il fascio di circonferenze di equazione x2 + y2 + (2 – k) x + (k – 8) y – 3 + k = 0 e studia le sue caratteristiche. Trova per quali valori di k si ha la circonferenza: a) passante per l’origine; b) di raggio uguale a ; c) tangente all’asse y; d) con il centro che ha distanza dall’origine minore di 5/2 .
Studia le caratteristiche del fascio di circonferenze di equazione x2 + y2 — 2(k — 3)x + ky— 6k + 14 = 0. a) Stabilisci per quali valori di k l’equazione rappresenta una circonferenza. b) Determina per quali valori di k si hanno le circonferenze del fascio che incontrano l’asse delle y in due punti A e B tali che AB = √56.