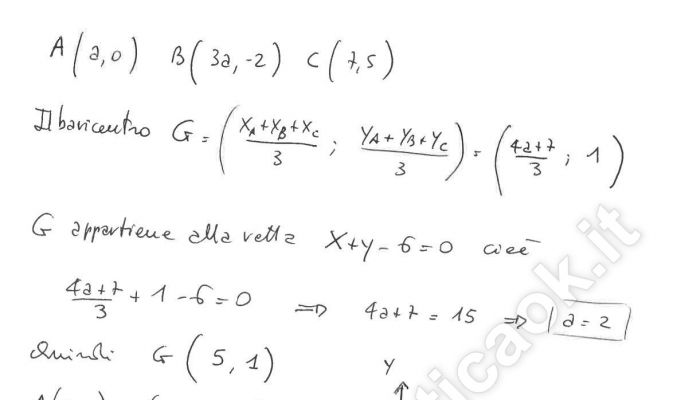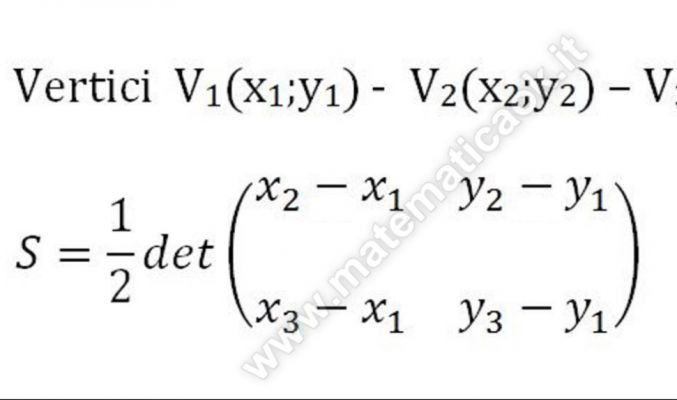Baricentro – Circocentro – Excentro – Incentro – Ortocentro
Il baricentro di un triangolo è il punto di incontro delle tre mediane. Il circocentro di un triangolo è il punto di incontro dei tre assi. Gli excentri di un triangolo sono 3 e sono i punti d’incontro delle bisettrici degli angoli esterni al triangolo. L’incentro di un triangolo è il punto di incontro delle tre bisettrici. L’ortocentro di un triangolo è il punto di incontro delle tre altezze.
Esercizio 17 – Fascio di rette
Nel triangolo di vertici A(a ; 0), B(3a ; -2), C(7 ; 5) il baricentro appartiene alla retta x + y – 6 = 0. Verificare che il triangolo è isoscele e che la distanza tra il baricentro e il circocentro è 1/6 della base AB.
Area di un triangolo noti i tre vertici
Esercizio 16 – Fascio di rette
È dato il fascio di rette di equazione (k – 1) x + (k + 1) y + 2 – k = 0 a) Calcolare le coordinate del centro C del fascio; b) verificare che la retta r del fascio perpendicolare alla retta t di equazione 3x – y = 0 passi per l’origine O del sistema di riferimento; c) calcolare le coordinate dei punti A e B in cui la…
Esercizio di geometria su angoli supplementari
Due angoli sono supplementari e il secondo angolo supera il doppio del primo di 15°. Calcola l’ampiezza di ciascun angolo.
Esercizio 4 – Calcolo di aree di figure piane
Data la parabola 9y = -4×2 + 24x e la retta y = x che la taglia nei punti A e B, trovare la misura dell’area della parte di piano limitata dalle tangenti in A e in B e dalla curva.
Esercizio 3 – Calcolo di aree di figure piane
Data la parabola di equazione y = -x2 + 5x – 4, calcolare la misura dell’area della minore delle due parti di piano limitate dall’asse x, dalla curva e dalla tangente alla curva nel punto di ascissa x=2.
Esercizio 2 – Calcolo di aree di figure piane
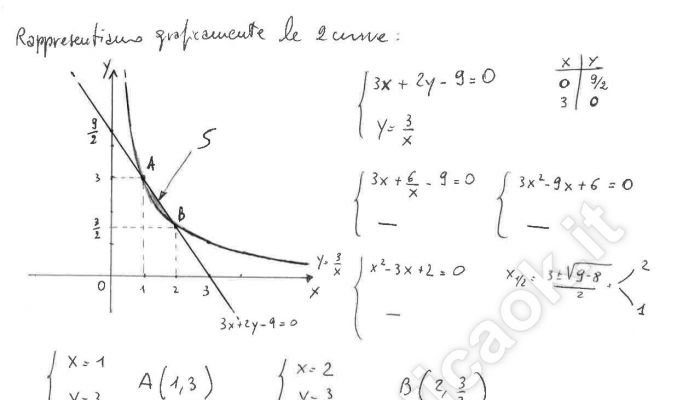
Si determinino le coordinate dei punti comuni alle due curve aventi le seguenti equazioni e si calcoli la misura dell’area della parte di piano limitata dagli archi delle due curve considerate: y=3/x e 3x+2y-9=0 aventi per estremi i punti A e B da trovare.