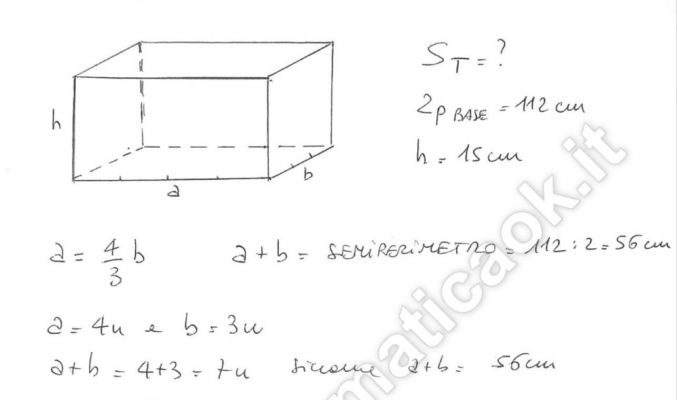
Le dimensioni di base di un parallelepipedo rettangolo sono una i 4/3 dell’altra. Calcola l’area della superficie totale del parallelepipedo, sapendo che è alto 15cm e che il perimetro di base è 112 cm.
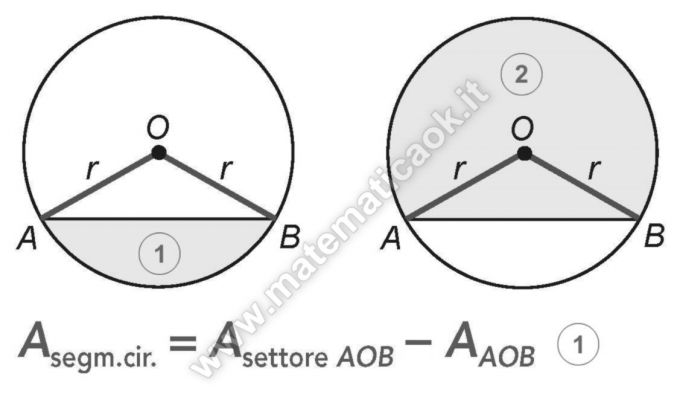
Area del segmento circolare: Teoria
L’area del segmento circolare a una base che non contiene – 1 – (o contiene – 2 -) il centro del cerchio è uguale alla differenza (o alla somma) tra l’area del settore circolare che insiste sul suo stesso arco e l’area del triangolo i cui lati sono due raggi e la corda che sottende l’arco.
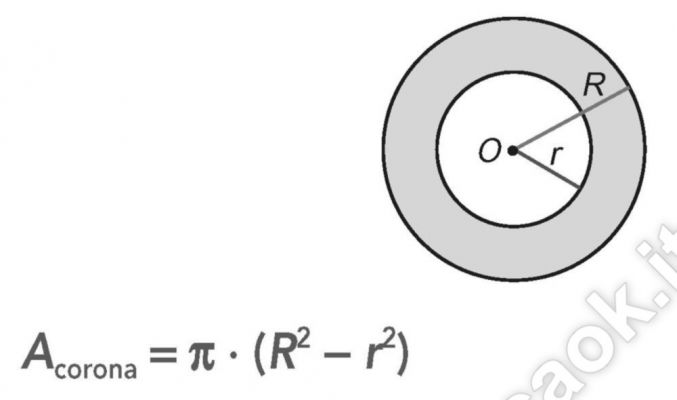
Corona circolare e Settore circolare: Teoria
L’area della corona circolare è uguale alla differenza delle aree dei due cerchi concentrici che la delimitano. L’area del settore circolare è direttamente proporzionale alla sua ampiezza e il cerchio si può considerare il settore di ampiezza massima, cioè di 360°; ovvero l’area del settore circolare è uguale al semiprodotto del raggio e dell’arco corrispondente.
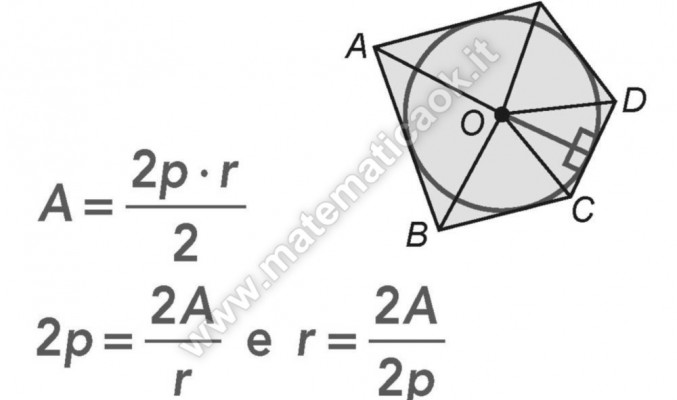
Area di un poligono circoscritto a una circonferenza:Teoria
L’area di un poligono circoscritto a una circonferenza si calcola moltiplicando la misura del perimetro del poligono per quella raggio della circonferenza e dividendo il risultato per 2.
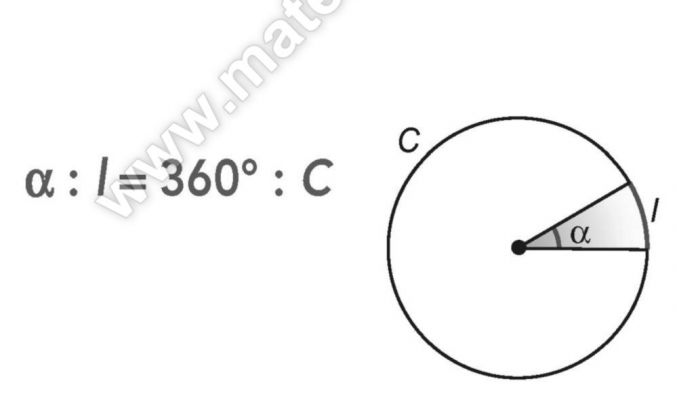
Misura della circonferenza e dell’arco di circonferenza: Teoria
Il rapporto tra la misura della circonferenza e il diametro è espresso con la lettera greca ed il suo valore approssimato a meno di 0,01 è 3,14. La misura della circonferenza si ottiene moltiplicando la misura del diametro per , oppure il raggio per 2. L’ampiezza degli angoli al centro e la lunghezza degli archi corrispondenti sono grandezze direttamente proporzionali.
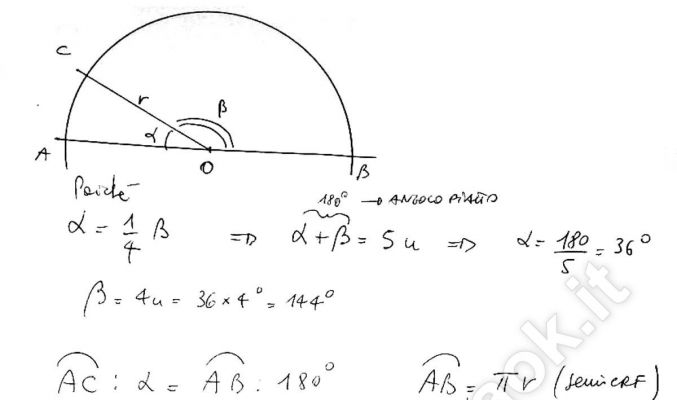
Esercizio 5 – Cerchio, settori circolari
Un semicerchio cerchio è diviso in 2 settori circolari che sono uno 1/4 dell’altro. Sapendo che il raggio misura 18 cm, trovare l’ampiezza e l’area dei due settori.
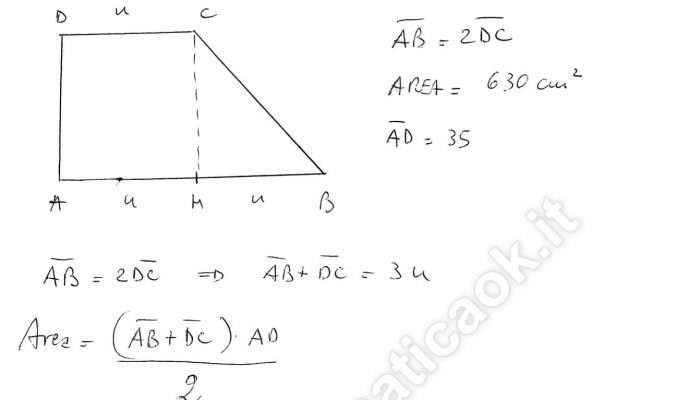
Esercizio 4 – Trapezio rettangolo – Richiesto online
In un trapezio rettangolo la base maggiore è doppia della minore. Sapendo che l’area è 630 cm2 e che l’altezza misura 35 cm, calcola il perimetro del trapezio.
Esercizio 3 – Triangolo isoscele – Richiesto online
Il perimetro di un triangolo isoscele è 96 cm. Calcola la misura dell’area del triangolo sapendo ke la base è i 6/5 del lato obliquo e che l’altezza relativa a quest’ultimo è i 4/5 della base.
Esercizio 19 – Fascio di circonferenze
Studia il fascio di circonferenze di equazione x2 + y2 – (2 + k) x + (k – 2) y + 2 = 0 indicando le sue caratteristiche. Trova poi la circonferenza del fascio: a) tangente all’asse x; b) che racchiude un’area 8; c) il cui centro appartiene alla retta y = 2x – 5; d) tangente alla retta y = x – 4.
Esercizio 18 – Fascio di circonferenze
Studia il fascio di circonferenze x2 + y2 – 2x + 4y + k(x + y – 20) = 0. Quale circonferenza del fascio ha il centro nell’origine degli assi? Scrivi l’equazione del fascio di circonferenze simmetrico al fascio dato rispetto all’asse x e trova per quali valori di k si hanno nei due fasci le circonferenze con il centro rispettivamente sull’asse y e sull’asse x.