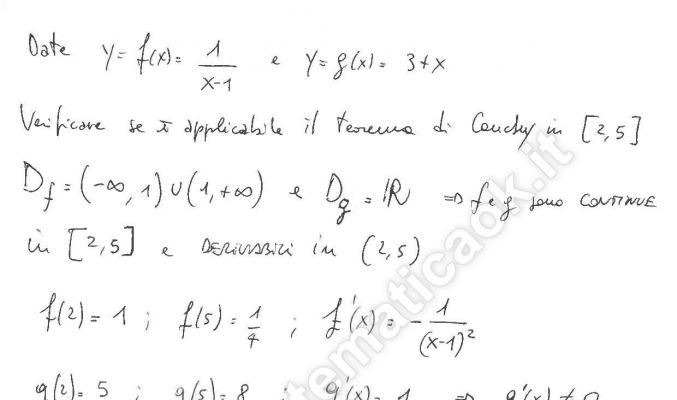Month: Novembre 2015
Esercizio 4 – Teorema di Cauchy: applicazioni
Esercizio 3 – Teorema di Cauchy: applicazioni
Esercizio 2 – Teorema di Cauchy: applicazioni
Geometria piana: formule
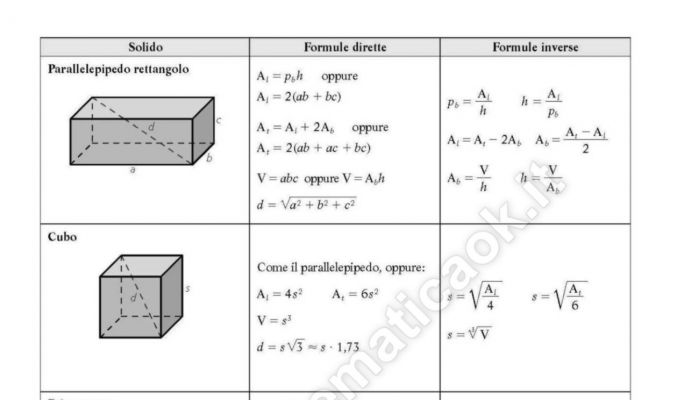
Geometria solida: formule
Esercizio 19 – Fascio di rette
Dato il fascio di rette di equazione (2 + k) x + (k – 1) y + 3 – k = 0, determinare: 1) le coordinate del centro del fascio; 2) il valore di k per cui vi è una retta del fascio parallela alla retta passante per A (2 ; 1) e per B(0 ; 3) e giustificare il risultato ottenuto; 3) i valori di k per i quali…
Esercizio 18 – Fascio di rette
Dopo aver calcolato le coordinate del centro del fascio di rette di equazione (l + k) x + (2 – k) y – 4 – k = 0, determinare per quali valori di k la retta del fascio: 1) è perpendicolare alla retta x + 5y — 3 = 0; 2) passa per il punto di intersezione delle rette x + 3y-5 = 0 e 2x-y + 4 = 0.
Esercizio 1 – Teorema di Cauchy: applicazioni
Baricentro – Circocentro – Excentro – Incentro – Ortocentro
Il baricentro di un triangolo è il punto di incontro delle tre mediane. Il circocentro di un triangolo è il punto di incontro dei tre assi. Gli excentri di un triangolo sono 3 e sono i punti d’incontro delle bisettrici degli angoli esterni al triangolo. L’incentro di un triangolo è il punto di incontro delle tre bisettrici. L’ortocentro di un triangolo è il punto di incontro delle tre altezze.