Un quadrilatero (o quadrangolo) è un poligono di quattro lati. Due lati non consecutivi di un quadrilatero sono detti opposti. Due angoli interni di un quadrilatero non adiacenti ad uno stesso lato sono detti opposti. Esistono quadrilateri concavi e quadrilateri convessi. Proprietà dei quadrilateri convessi: 1) ha 4 angoli interni 2) la somma degli angoli interni è un angolo giro (360°); 3) la somma degli angoli esterni è uguale a quella…
geometria piana
Esercizio 28 – Rettangolo inscritto in triangolo rettangolo
Un triangolo ABC rettangolo in A ha i cateti AB e AC rispettivamente di lunghezza 20 cm e 15 cm. Determina sull’ipotenusa un punto P in modo che, dette H e K le sue proiezioni sui cateti, il rettangolo PHAK abbia perimetro 36 cm.
Esercizio 26 – Triangolo rettangolo e teoremi di Euclide
In un triangolo rettangolo l’ipotenusa misura 30 cm e il rapporto delle proiezioni dei cattivi su di essa è 16 / 9. Quanto misurano l’altezza relativa all’ipotenusa ed il perimetro del triangolo?
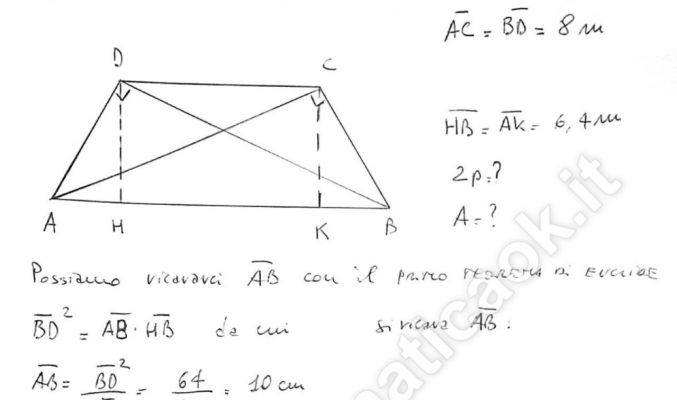
Esercizio 27 – Trapezio isoscele e teoremi di Euclide
Nel trapezio isoscele ABCD le diagonali sono perpendicolari ai lati obliqui e ognuna di esse misura 8 metri. Calcola il perimetro e l’area del trapezio sapendo che le proiezioni delle diagonali sulla base maggiore sono lunghe ciascuna 6,4 metri.
Esercizio 25 – Rettangolo e primo teorema di Euclide
Nel rettangolo ABCD, la diagonale BD misura 95 cm ed è divisa dalla perpendicolare AH, condotta per il vertice A, in due segmenti tali che uno di essi è 9/16 dell’altro. Calcola il perimetro e l’area del rettangolo.
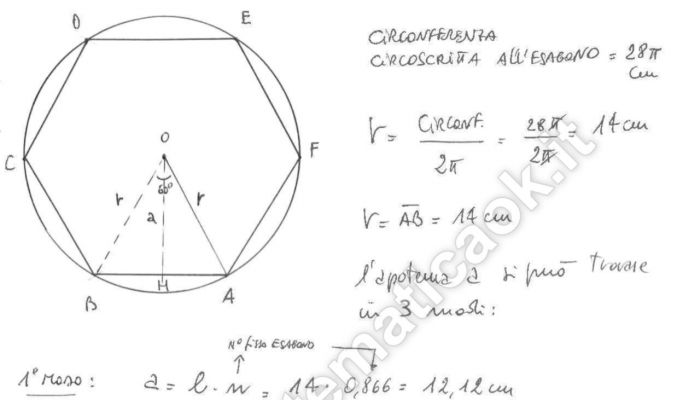
Esercizio 24 – Esagono regolare inscritto in circonferenza
Un esagono regolare è inscritto in una circonferenza lunga 28 cm. Calcola l’area dell’esagono.
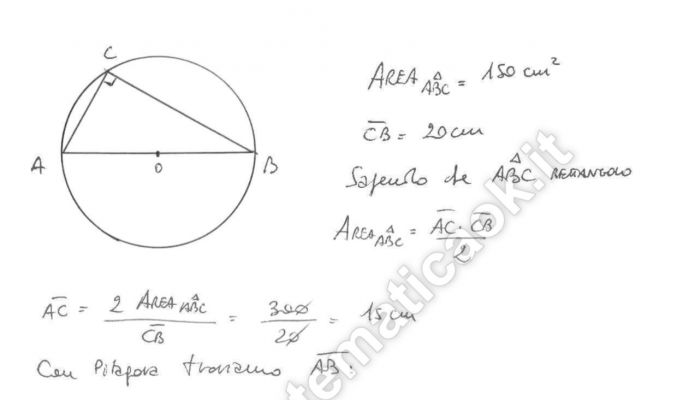
Esercizio 23 – Triangolo rettangolo inscritto in circonferenza
Un triangolo rettangolo ha l’area di 150 cm2 e un cateto lungo 20 cm. Calcola la lunghezza della circonferenza circoscritta al triangolo.
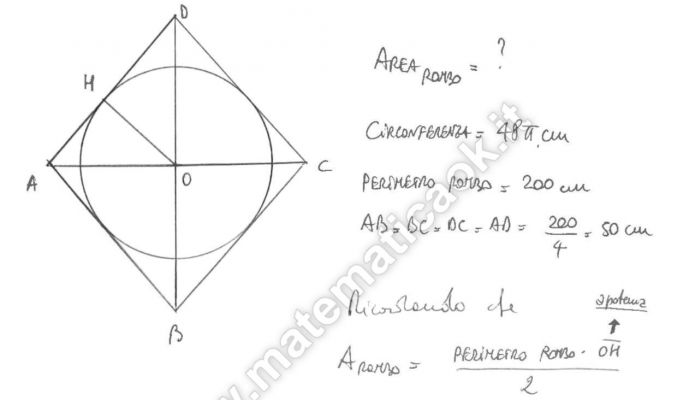
Esercizio 22 – Rombo circoscritto a circonferenza
Un rombo è circoscritto a una circonferenza lunga 48 cm. Calcolare l’area del rombo, sapendo che il perimetro misura 200 cm.
Esercizio 21 – Spirale a cerchi
Osserva attentamente la figura e costruisci una spirale partendo da un segmento a piacere AB. Per ottenere le altre circonferenze dovrai puntare alternativamente in A o in B. Calcola la lunghezza del contorno disegnato più spesso e l’area della parte colorata.
Esercizio 20 – Cerchi
La figura rappresenta un motivo ornamentale noto. Sapendo che AB = 4 cm, AO = OB e AB = BC, calcola il perimetro e l’area della superficie colorata.