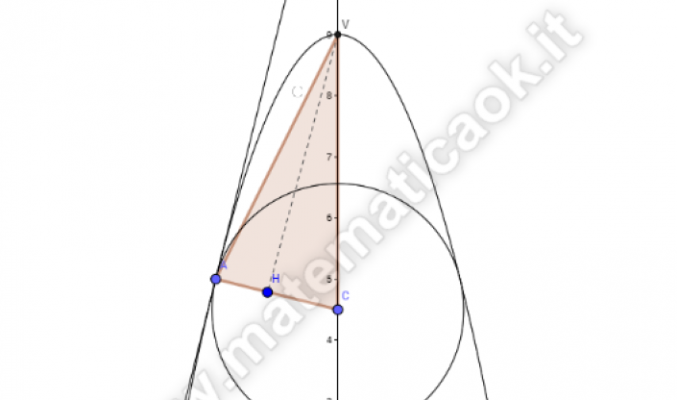
Determina e rappresenta l’equazione della parabola con asse parallelo all’asse y con vertice in V(0; 9) e passante per A ( — 2; 5). Successivamente trova e rappresenta l’equazione della retta t tangente in A alla parabola. Scrivi l’equazione della circonferenza con il centro C sull’asse y e tangente in A alla retta t e rappresentala graficamente. Detto V il vertice della parabola, calcola l’area del triangolo A VC.
esercizi svolti
Esercizio 24 – Fascio di parabole
Studia il fascio di parabole di equazione (m + 1) x2 — 4 (m + 1) x — (m + 1) y + 4 + 5m = 0 e determinare poi la parabola del fascio: a) passante per il punto A(3; — 3); b) che intercetta sull’asse delle ascisse un segmento di lunghezza 6; c) tangente alla retta 2x — y — 3 = 0; d) che forma nel I…
Esercizio 16 – Solido composto da due cubi sovrapposti – richiesto online da Martina
Un solido è formato da due cubi sovrapposti i cui spigoli misurano rispettivamente 12 cm e 7 cm. Calcola l’area della superficie totale e il volume del solido composto.
Esercizio 67 – Angoli interni di un triangolo – richiesto online da Stefano
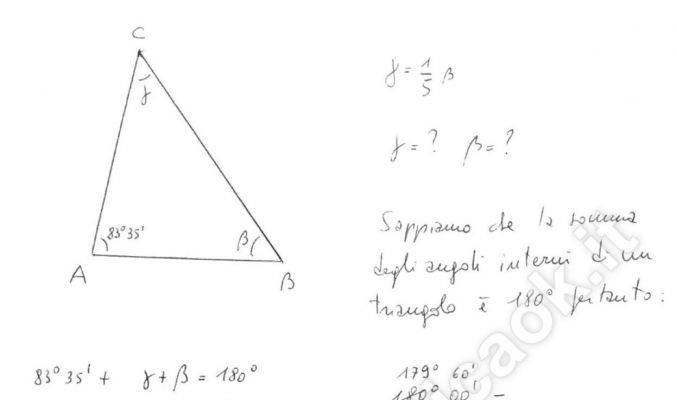
Un angolo ti triangolo misura 83° 35′. Sapendo che gli altri due angoli sono uno 1/5 dell’altro, calcola le misure incognite dei due angoli.
Esercizio 66 – Quadrilatero inscritto in circonferenza – richiesto online da Guglielmo
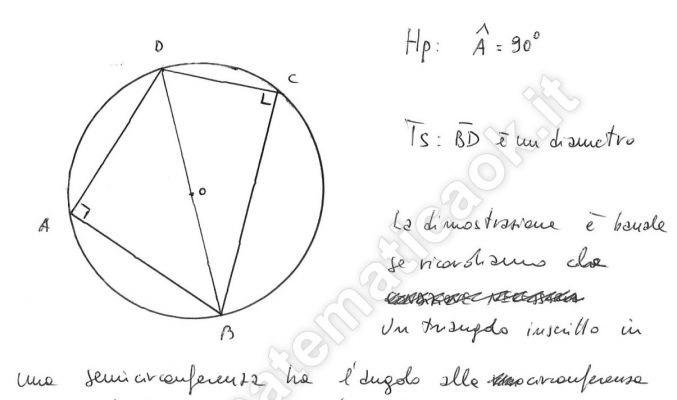
Dimostra che se un quadrilatero inscritto in una circonferenza ha un angolo retto, allora il centro della circonferenza appartiene a una diagonale del quadrilatero.
Esercizio 65 – Triangolo e quadrilatero inscritto – richiesto online da Guglielmo
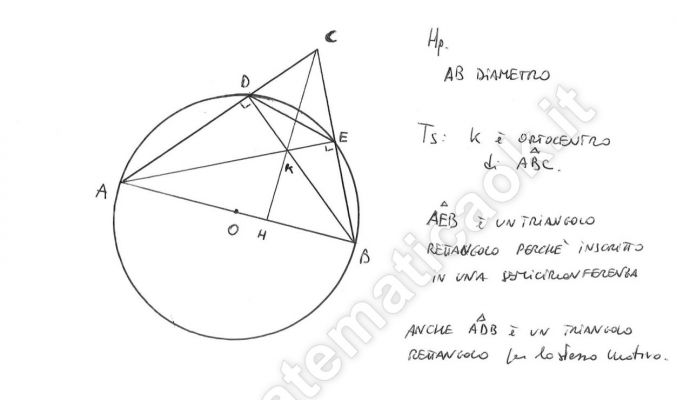
Considera il triangolo ABC con il lato AB coincidente con un diametro di una circonferenza e il vertice C esterno ad essa. Detti D ed E i punti di intersezione della circonferenza con i lati AC e BC, dimostrare che il punto di incontro delle diagonali del quadrilatero inscritto ABED coincide con l’ortocentro del triangolo ABC.
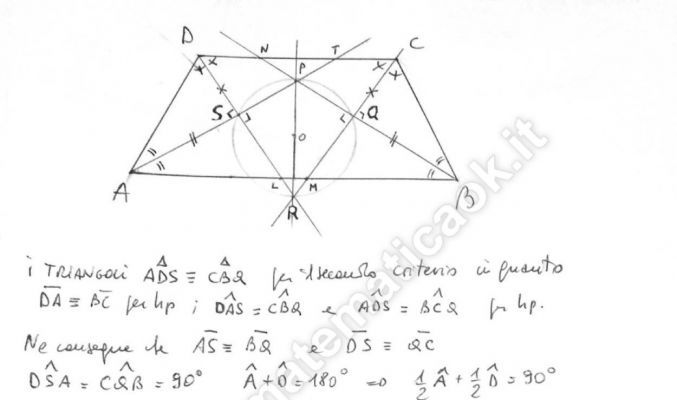
Esercizio 64 – Bisettrici di un trapezio isoscele – richiesto online da Guglielmo
Dimostrare che, se i punti di intersezione delle bisettrici degli angoli di un trapezio isoscele sono vertici di un quadrilatero, questo è inscrittibile in una circonferenza.
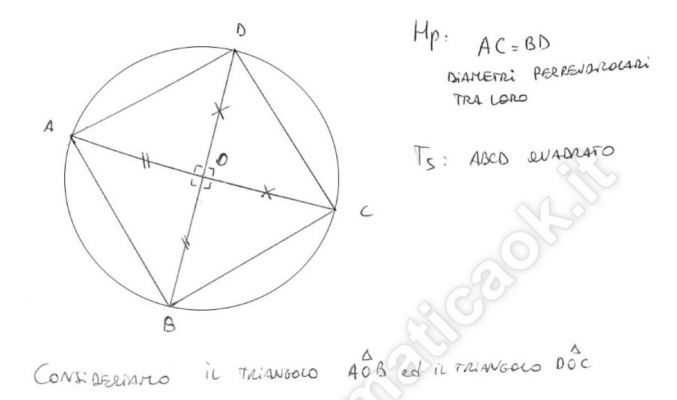
Esercizio 63 – Quadrato inscritto – richiesto online da Guglielmo
Siano AC e BD due diametri perpendicolari di una circonferenza di centro O. Dimostrare che A, B, C e D sono i vertici di un quadrato.
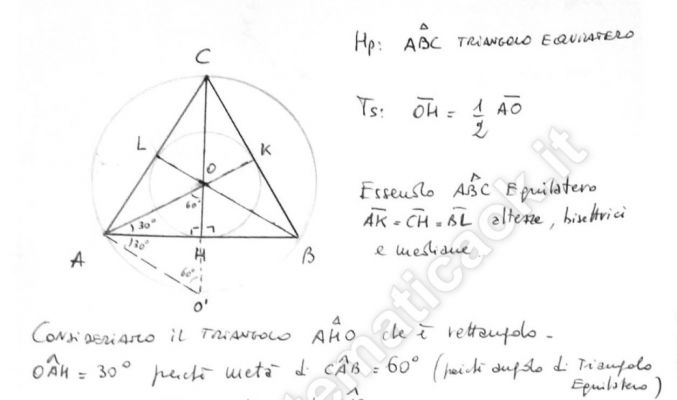
Esercizio 62 – Triangolo equilatero inscritto in circonferenza – richiesta online di Paolo
Dimostrare che il raggio del cerchio circoscritto ad un triangolo equilatero e il doppio del raggio del cerchi inscritto.
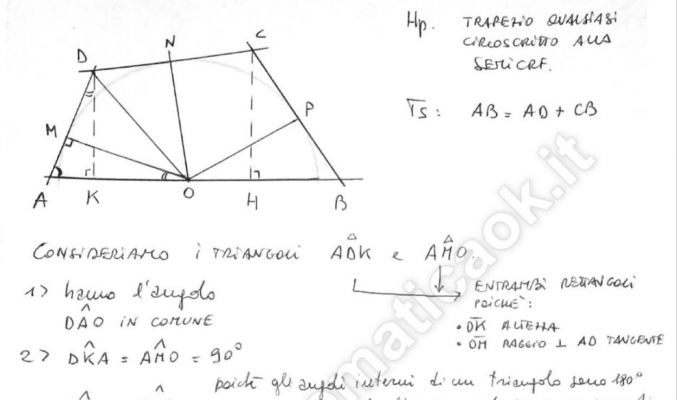
Esercizio 61 – Trapezio circoscritto ad una semicirconferenza – richiesto online da Paolo
Dimostrare che la base maggiore di un trapezio circoscritto ad una semicirconferenza e congruente alla somma dei lati obliqui.