insiemi
Operazioni sugli insiemi: PRODOTTO CARTESIANO
Dati due insiemi A e B non vuoti, definiamo prodotto cartesiano di A e B (nell’ordine) l’insieme delle coppie ordinate (a,b) con a∈A e b∈B; cioè A×B = {(a;b) | a∈A e b∈B}
Operazioni sugli insiemi: COMPLEMENTARE
Sia U un insieme qualunque ed A un suo sottoinsieme A ⊆ U. Si dice complementare di A in U e si indica con CU A o anche , l’insieme degli elementi di U che non appartengono ad A
Operazioni sugli insiemi: DIFFERENZA SIMMETRICA
Operazioni sugli insiemi: DIFFERENZA
Dati due insiemi A e B, si dice differenza fra A e B l’insieme formato dagli elementi di A che non appartengono a B e lo denotiamo con A \ B o A – B. Analogamente la differenza fra B ed A è l’insieme formato dagli elementi di B che non appartengono ad A e lo denotiamo con B \ A o B – A. Si deduce che A – B ≠ B – A
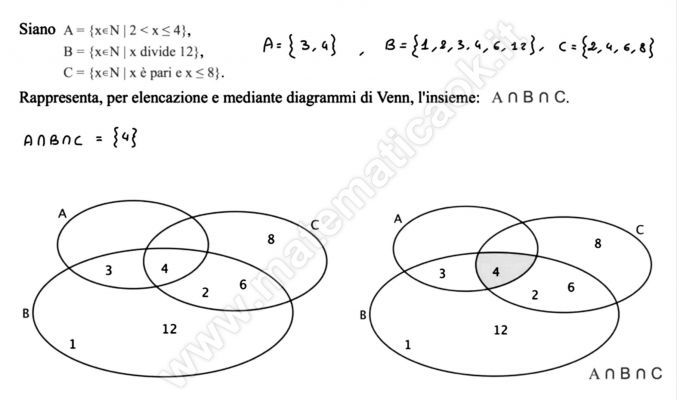
Operazioni sugli insiemi: INTERSEZIONE
Dati due insiemi A e B definiamo intersezione di A e B l’insieme formato dagli elementi che appartengono sia ad A che a B e lo denotiamo con A ∩ B. Due insiemi A e B si dicono disgiunti quando A ∩ B = ∅
Operazioni sugli insiemi: UNIONE
Dati due insiemi A e B definiamo unione di A e B l’insieme formato dagli elementi che appartengono ad A o a B o a entrambi e lo denotiamo con A ∪ B
Sottoinsiemi ed Insieme delle Parti
Dati due insiemi A e B, si dice che B è sottoinsieme di A se ogni elemento di B è anche elemento di A e si indica B ⊆ A –> si legge anche B è contenuto o è incluso in A. Osservazione Due insiemi A e B si dicono uguali se sono formati con gli stessi elementi A = B ovvero ogni elemento dell’uno è anche elemento dell’altro (non ha…
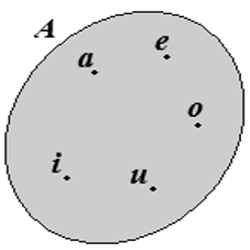
Insiemi: definizione e rappresentazione
Definizione Il concetto di insieme si assume come primitivo, cioè non riconducibile a concetti precedentemente definiti. Sinonimi di insieme sono: collezione, aggregato, classe, ecc. E’ importante che esista un criterio atto a stabilire in modo univoco se un elemento appartiene o no all’insieme. Ad esempio l’insieme delle vocali dell’alfabeto latino è un insieme, mentre l’insieme dei libri divertenti non è un insieme perché il criterio per stabilire se un libro…