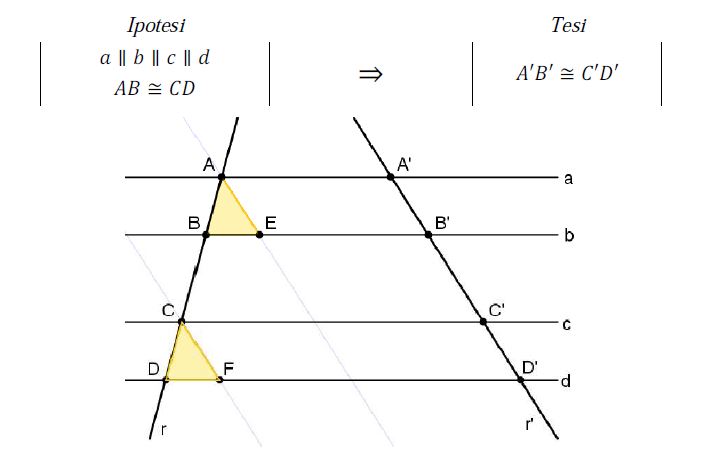
Dato un fascio di rette parallele tagliate da due trasversali, a segmenti congruenti su una trasversale corrispondono segmenti congruenti sull’altra trasversale.
Dimostrazione:
Conduciamo da A la parallela ad r’ e indichiamo con E il suo punto d’intersezione con b
Conduciamo da C la parallela ad r’ e indichiamo con F il suo punto d’intersezione con d
I due triangoli ABE e CDF sono congruenti per il II criterio di congruenza dei triangoli
Pertanto AE ≅ CF
Ma AEB’A’ e CFD′C′ sono due parallelogrammi (hanno i lati opposti paralleli)
Di conseguenza: A′B′ ≅ AE e CF ≅ C′D′
Per la proprietà transitiva si ha: A′B′ ≅ C′D′