Data la semicirconferenza di diametro AB=2, considera il punto P appartenente a essa e tale che l’angolo PBA=x; traccia la tangente in P, e sia H la proiezione del punto B sulla tangente. Determina la funzione f(x) = PH + HB e traccia il suo grafico ed evidenzia la parte relativa al problema.
trigonometria
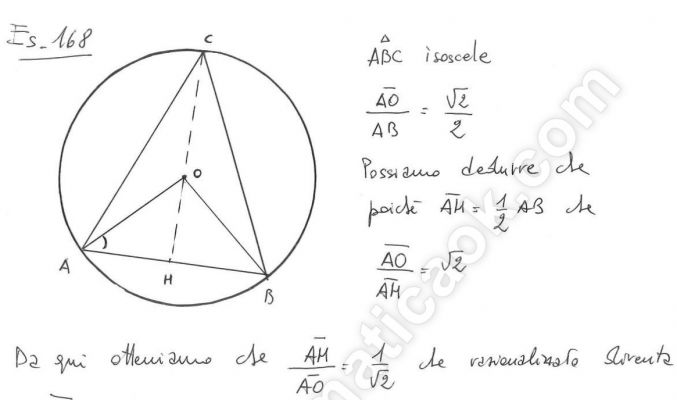
Es. 168 – Triangolo isoscele iscritto in una circonferenza
Nel triangolo isoscele ABC il rapporto tra il raggio della circonferenza circoscritta e la base AB è √2/2 . Trovare l’ampiezza dell’angolo al vertice ACB.
Esercizio 178 – Quadrilatero ABCD inscritto in circonferenza
Il quadrilatero ABCD è inscritto in una circonferenza di raggio r e AB=BC, l’angolo ABC=60°. Posto l’angolo ACD=x a)dimostra che AD+CD=BD b)esprimi la funzione f(x)=CD/BD e trova per quali valori di x risulta f(x)=1/2
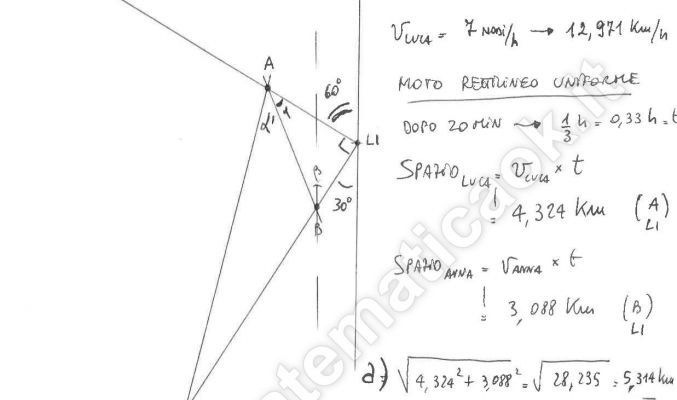
Esercizio 5 – Trigonometria
Anna e Luca partono con le loro barche a vela (nello stesso istante) dal porto di Livorno (LI) in direzioni tra loro perpendicolari: Anna è diretta verso Bastia (BT) mentre Luca è diretto verso Savona (SV). Le velocità delle due imbarcazioni sono rispettivamente 5 nodi e 7 nodi (1 nodo = 1 miglio marino (1,853 km/h). La distanza tra Livorno e Bastia è 117 km. Anna orienta quindi la rotta verso Sud 30°…
Esercizio 4 – Trigonometria
Un triangolo ha un lato di misura a ed ha uno degli angoli adiacenti a esso che è uguale al doppio dell’altro. Calcolare quest’ultimo sapendo che la misura dell’area del triangolo è (a2 √3)/8.
Esercizio 3 – Trigonometria
Un triangolo ha il perimetro di misura 4a(2 + √2 + √6) e due angoli misurano rispettivamente 45° e 60°. Trovare la misura dei tre lati.
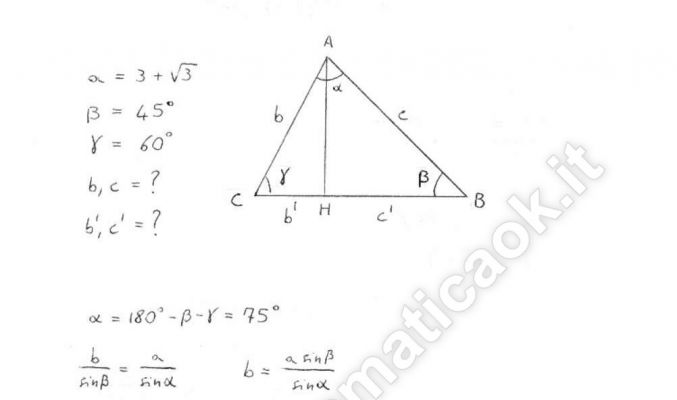
Esercizio 2 – Trigonometria
Un triangolo ha un lato che misura 3 + √3 e gli angoli a esso adiacenti di 45° e 60°. Trovare le misure degli altri due lati e i segmenti in cui la base data viene divisa dall’altezza a essa relativa.
Esercizio 1 – Trigonometria
Nel triangolo ABC i lati AB e BC sono lunghi, rispettivamente, 13 cm e √673 cm, mentre la mediana relativa al lato AC è lunga 15 cm. Determinare la lunghezza del lato AC e il coseno dell’angolo BAC.
Trigonometria: Area di un triangolo qualsiasi
Trigonometria: Teorema del coseno o di Carnot
Può essere considerato una generalizzazione del Teorema di Pitagora sui triangoli non rettangoli. a2 = b2 + c2 – 2 b c cosα b2 = a2 + c2 – 2 a c cosβ c2 = a2 + b2 – 2 a b cosγ