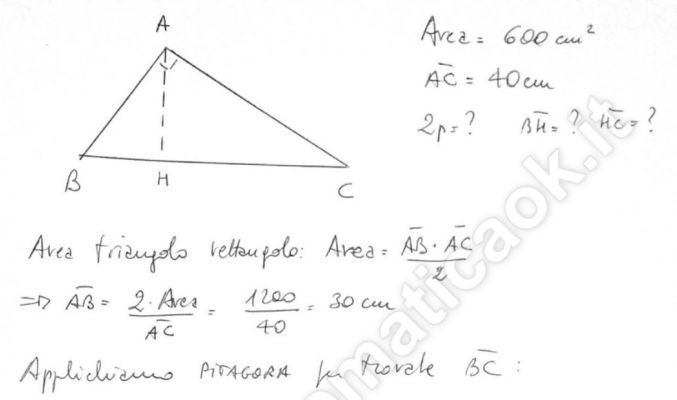
In un triangolo rettangolo l’area misura 600 cm quadrati e un cateto è lungo 40 cm. Calcola il perimetro e la lunghezza delle due proiezioni dei cateti sull’ipotenusa.
triangolo rettangolo
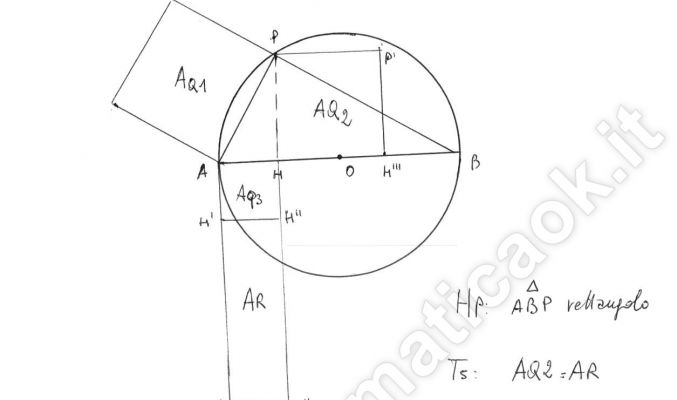
Esercizio 60 – Dimostrazione secondo teorema di Euclide – richiesto online da Guglielmo
Sia P un punto della circonferenza di diametro AB. Da P conduci la perpendicolare PH ad AB. Dimostra che il quadrato costruito su PH è equivalente al rettangolo di lati AH e HB.
Esercizio 56 – Triangolo rettangolo – richiesto online da Mario
In un triangolo rettangolo l’ipotenusa misura 244 cm e il cateto minore è i suoi 11/61. Calcola perimetro e area del triangolo.
Esercizio 32 – Cerchio e triangoli rettangoli
Da un punto P esterno ad una circonferenza di centro O, si conducano le rette tangenti alla circonferenza stessa che la incontrano nei punti A e B. Sapendo che P dista dal centro 40 cm e che i segmenti di tangenza sono 2/3 del diametro, calcola il perimetro del triangolo APB.
Esercizio 28 – Rettangolo inscritto in triangolo rettangolo
Un triangolo ABC rettangolo in A ha i cateti AB e AC rispettivamente di lunghezza 20 cm e 15 cm. Determina sull’ipotenusa un punto P in modo che, dette H e K le sue proiezioni sui cateti, il rettangolo PHAK abbia perimetro 36 cm.
Esercizio 26 – Triangolo rettangolo e teoremi di Euclide
In un triangolo rettangolo l’ipotenusa misura 30 cm e il rapporto delle proiezioni dei cattivi su di essa è 16 / 9. Quanto misurano l’altezza relativa all’ipotenusa ed il perimetro del triangolo?
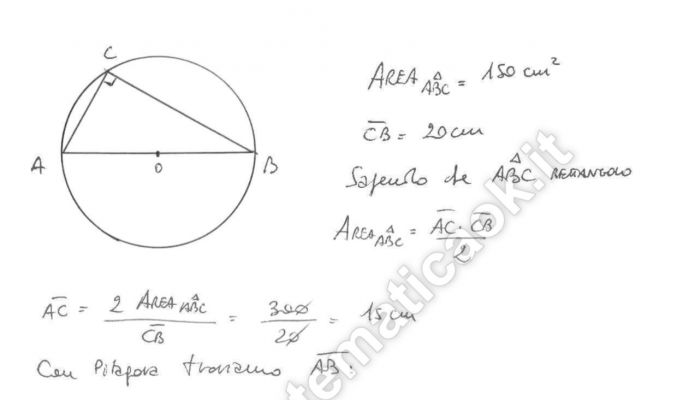
Esercizio 23 – Triangolo rettangolo inscritto in circonferenza
Un triangolo rettangolo ha l’area di 150 cm2 e un cateto lungo 20 cm. Calcola la lunghezza della circonferenza circoscritta al triangolo.
Raggio del cerchio inscritto in un triangolo rettangolo
Inscrivibilità in una semicirconferenza
Un triangolo rettangolo si può sempre inscrivere in una semicirconferenza; ne consegue che la mediana relativa all’ipotenusa è la metà dell’ipotenusa ed è il raggio del cerchio circoscritto.
Secondo Teorema di Euclide
In un triangolo rettangolo, il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha per dimensioni le proiezioni dei cateti sull’ipotenusa. Ovvero CH2 = AH . HB