geometria piana
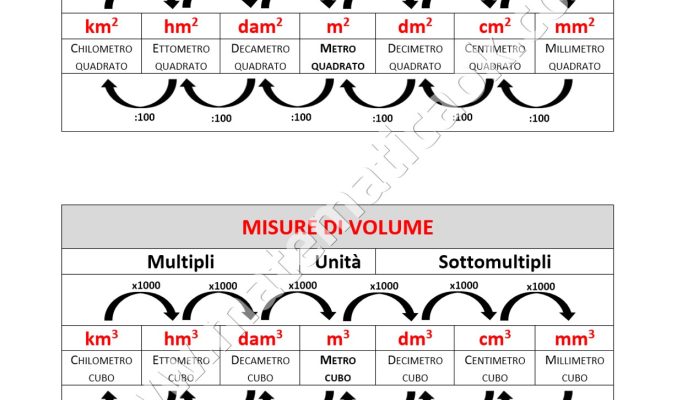
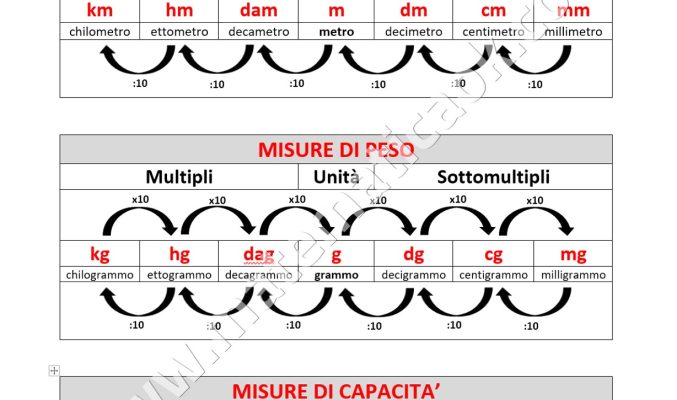
Tabella Equivalenze lunghezza – peso – capacità
Es. 246 – Semicirconferenza di diametro AB=2
Data la semicirconferenza di diametro AB=2, considera il punto P appartenente a essa e tale che l’angolo PBA=x; traccia la tangente in P, e sia H la proiezione del punto B sulla tangente. Determina la funzione f(x) = PH + HB e traccia il suo grafico ed evidenzia la parte relativa al problema.
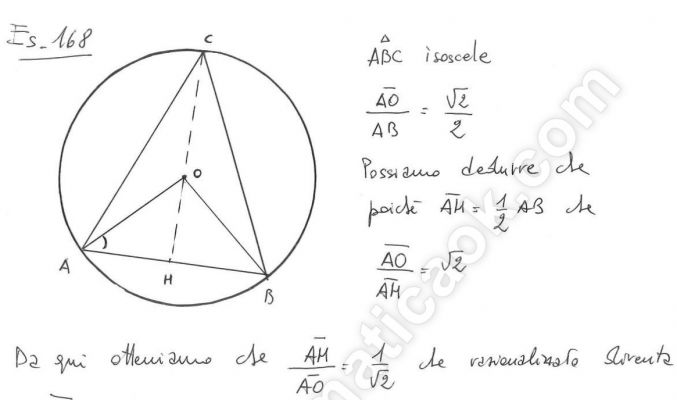
Es. 168 – Triangolo isoscele iscritto in una circonferenza
Nel triangolo isoscele ABC il rapporto tra il raggio della circonferenza circoscritta e la base AB è √2/2 . Trovare l’ampiezza dell’angolo al vertice ACB.
Esercizio 178 – Quadrilatero ABCD inscritto in circonferenza
Il quadrilatero ABCD è inscritto in una circonferenza di raggio r e AB=BC, l’angolo ABC=60°. Posto l’angolo ACD=x a)dimostra che AD+CD=BD b)esprimi la funzione f(x)=CD/BD e trova per quali valori di x risulta f(x)=1/2
Esercizio 70 – Perimentro di un rombo – richiesto online da Chiara
In un rombo la diagonale maggiore misura 50 cm ed è i 25/24 della diagonale minore. Calcola il perimetro del rombo.
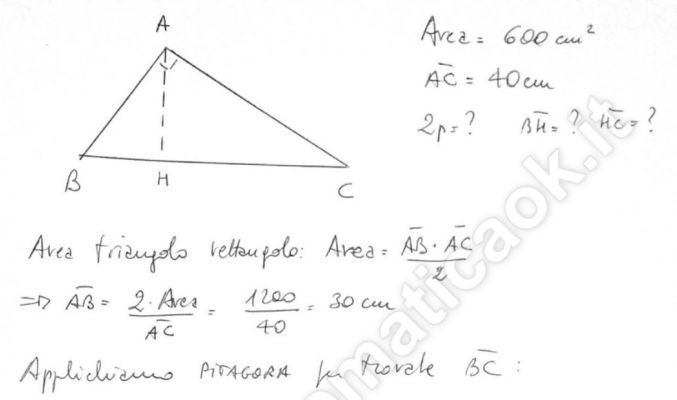
Esercizio 69 – Triangolo rettangolo e primo teorema di Euclide richiesto online da Chiara
In un triangolo rettangolo l’area misura 600 cm quadrati e un cateto è lungo 40 cm. Calcola il perimetro e la lunghezza delle due proiezioni dei cateti sull’ipotenusa.
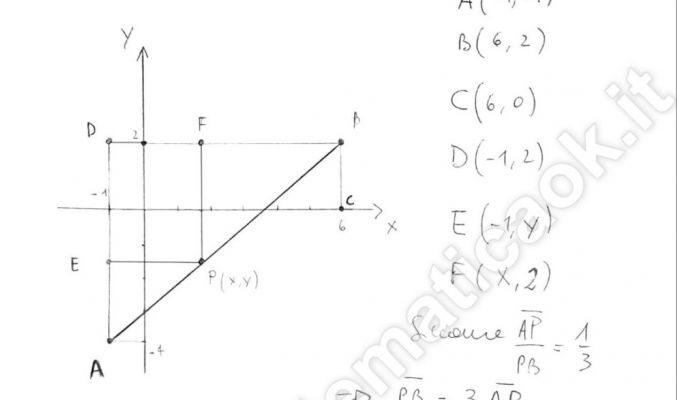
Esercizio 68 – Rapporto tra segmenti – Talete – richiesto online da Paolo
DATO IL SEGMENTO DI ESTREMI A(-1,-4) e B(6,2), DETERMINA SUL SEGMENTO AB UN PUNTO P, TALE CHE AP/PB = 1/3.
Retta parallela ad un lato del triangolo – Conseguenza inversa di Talete
Retta parallela ad un lato del triangolo – Conseguenza di Talete
Se una retta parallela a un lato di un triangolo interseca gli altri due lati, li divide in segmenti proporzionali.