… soluzione ai tuoi problemi …
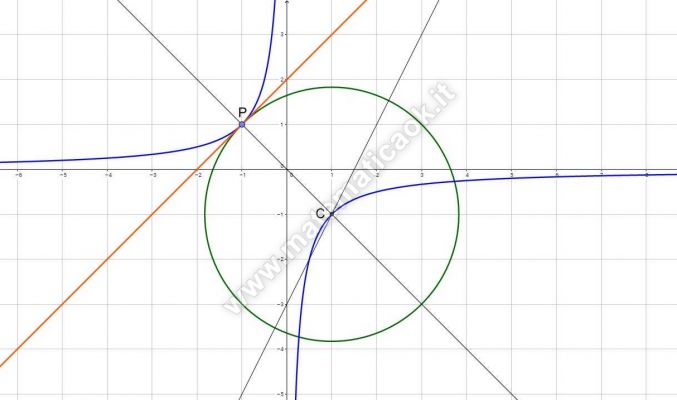
Scrivere l’equazione della circonferenza tangente alla retta y=x+2 nel punto P(-l;l) ed avente centro sulla retta di equazione 2x-y-3=0. Determinare poi l’equazione dell’iperbole equilatera riferita ai propri asintoti che passa per il centro della circonferenza.
Scrivere l’equazione della retta t, tangente nel punto T(2√6;2) appartenente all’iperbole di equazione: x^2 – 3y^2=12
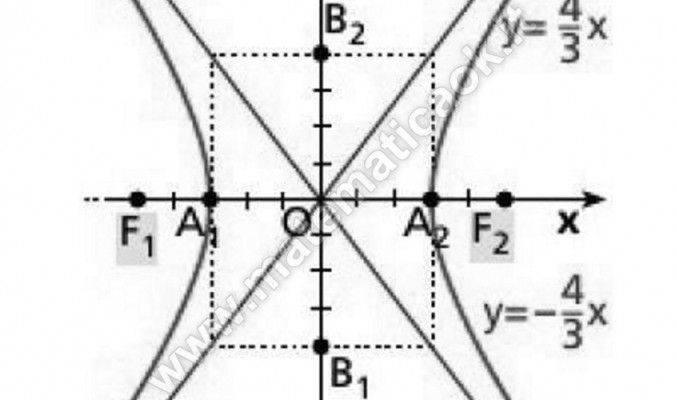
Scrivere l’equazione dell’iperbole, con asse focale coincidente con quello dell’asse x, sapendo che uno dei fuochi è il punto F(5/2;0) e un asintoto di equazione y=4/3x
Scrivere l’equazione dell’iperbole, con asse focale coincidente con quello dell’asse x, sapendo che b=3 e che uno dei fuochi è il punto F(-5;0)
Scrivere l’equazione dell’iperbole, con asse focale coincidente con quello dell’asse x, sapendo che a= 2√5 e passante per P (5;2)
