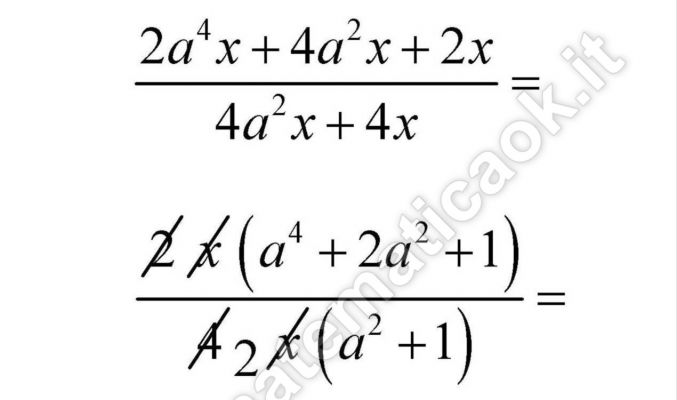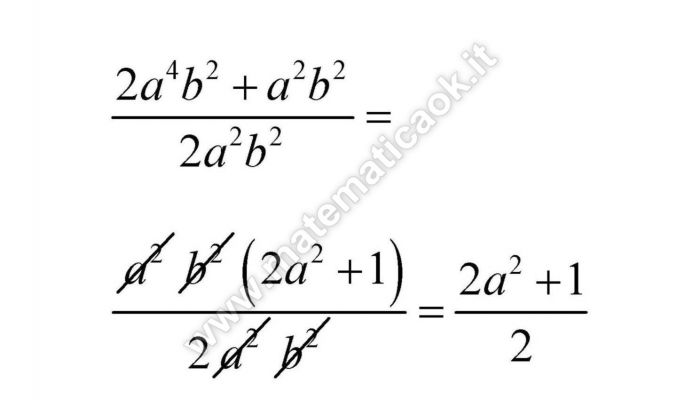Month: Dicembre 2015
Esercizio 5 – Frazioni algebriche
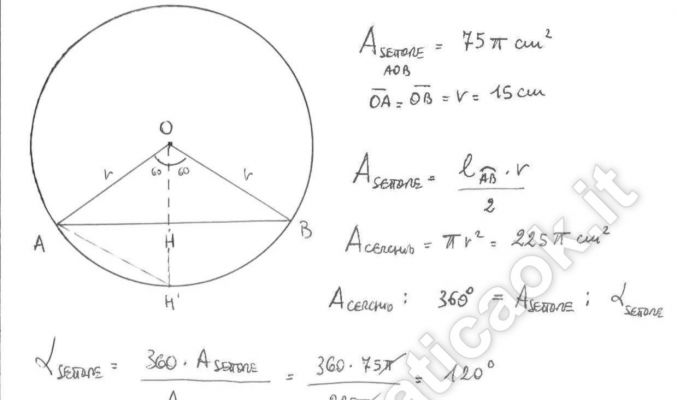
Esercizio 13 – Triangolo e circonferenza
Il triangolo AOB ha il vertice O nel centro della circonferenza e il lato AB è una corda che insiste sull’arco AB. Sapendo che il settore circolare AOB ha l’area di 75 cm2 e il raggio di 1 5 cm, calcola area e perimetro del triangolo.
Esercizio 4 – Trigonometria
Un triangolo ha un lato di misura a ed ha uno degli angoli adiacenti a esso che è uguale al doppio dell’altro. Calcolare quest’ultimo sapendo che la misura dell’area del triangolo è (a2 √3)/8.
Esercizio 3 – Trigonometria
Un triangolo ha il perimetro di misura 4a(2 + √2 + √6) e due angoli misurano rispettivamente 45° e 60°. Trovare la misura dei tre lati.
Esercizio 2 – Trigonometria
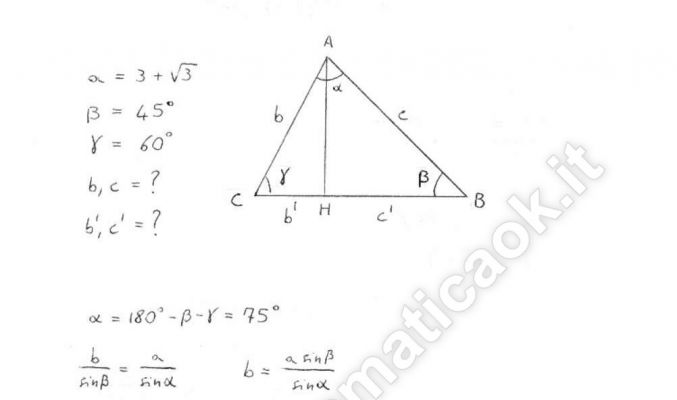
Un triangolo ha un lato che misura 3 + √3 e gli angoli a esso adiacenti di 45° e 60°. Trovare le misure degli altri due lati e i segmenti in cui la base data viene divisa dall’altezza a essa relativa.
Esercizio 1 – Trigonometria
Nel triangolo ABC i lati AB e BC sono lunghi, rispettivamente, 13 cm e √673 cm, mentre la mediana relativa al lato AC è lunga 15 cm. Determinare la lunghezza del lato AC e il coseno dell’angolo BAC.
Trigonometria: Area di un triangolo qualsiasi
Trigonometria: Teorema del coseno o di Carnot
Può essere considerato una generalizzazione del Teorema di Pitagora sui triangoli non rettangoli. a2 = b2 + c2 – 2 b c cosα b2 = a2 + c2 – 2 a c cosβ c2 = a2 + b2 – 2 a b cosγ
Trigonometria: Teorema dei seni
Noto anche come Teorema di Eulero, esprime una relazione di proporzionalità diretta fra le lunghezze dei lati di un triangolo e i seni dei rispettivi angoli opposti. dove R è il raggio del cerchio circoscritto al triangolo dato