Scrivere l’equazione dell’ellisse, con assi coincidenti con gli assi cartesiani, sapendo che uno dei fuochi è il punto F(–5;0) e passante per il vertice V(0;12)
geometria analitica
Esercizio 3 – Ellisse
Scrivere l’equazione dell’ellisse, con assi coincidenti con gli assi cartesiani, sapendo che b=4 e che uno dei fuochi è il punto F(3;0)
Esercizio 2 – Ellisse
Scrivere l’equazione dell’ellisse, con assi coincidenti con gli assi cartesiani, sapendo che a=5 e passante per il punto P(√5; –8√5/5)
Esercizio 1 – Ellisse
Determiniamo l’equazione di un’ellisse con fuochi sull’asse y che passa per il punto P(2; –5√5/3) ed ha eccentricità e = 4/5
Esercizio 5 – Iperbole
Scrivere l’equazione della retta t, tangente nel punto T(2√6;2) appartenente all’iperbole di equazione: x^2 – 3y^2=12
Esercizio 4 – Iperbole
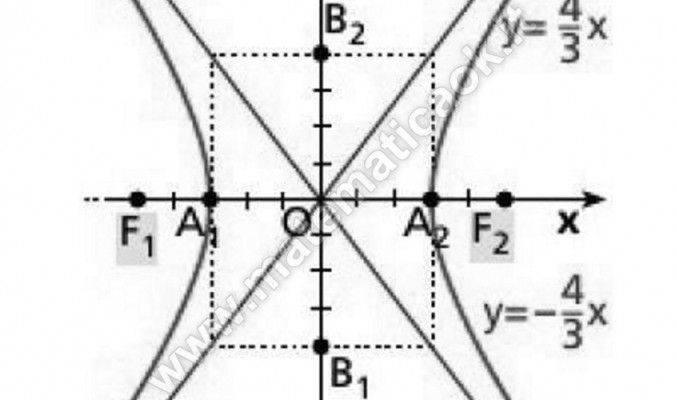
Scrivere l’equazione dell’iperbole, con asse focale coincidente con quello dell’asse x, sapendo che uno dei fuochi è il punto F(5/2;0) e un asintoto di equazione y=4/3x
Esercizio 3 – Iperbole
Scrivere l’equazione dell’iperbole, con asse focale coincidente con quello dell’asse x, sapendo che b=3 e che uno dei fuochi è il punto F(-5;0)
Esercizio 2 – Iperbole
Scrivere l’equazione dell’iperbole, con asse focale coincidente con quello dell’asse x, sapendo che a= 2√5 e passante per P (5;2)