Dopo aver rappresentato le parabole di equazioni x = 2y2 — 4y e x = 3y2 + 4, scrivi l’equazione del fascio da esse individuato, infine determina le parabole degeneri.
geometria analitica
Esercizio 19 – Fascio di parabole
Considera il fascio di parabole di equazione (m + 1) y2 + (m — 1) x + 2(m — 1) y = 0 e studia le sue principali caratteristiche. Determina poi la parabola del fascio: a) passante per il punto P(2; — 2); b) tangente alla retta x – 2y – 2 = 0; c) che intercetta sul semiasse positivo delle ordinate un segmento di lunghezza 2.
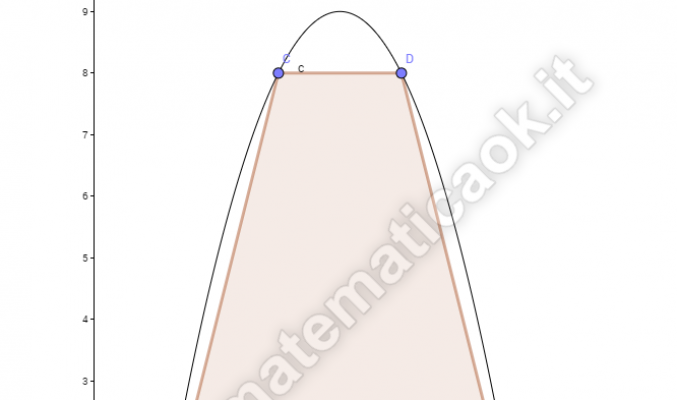
Esercizio 18 – Parabola e trapezio isoscele
Nella parte di piano definita dalla parabola di equazione y = — x2 + 8x — 7 e dall’asse x inscrivi un trapezio isoscele ABCD con la base maggiore AB sull’asse x. Trova le coordinate di C e D in modo che il trapezio abbia area 32.
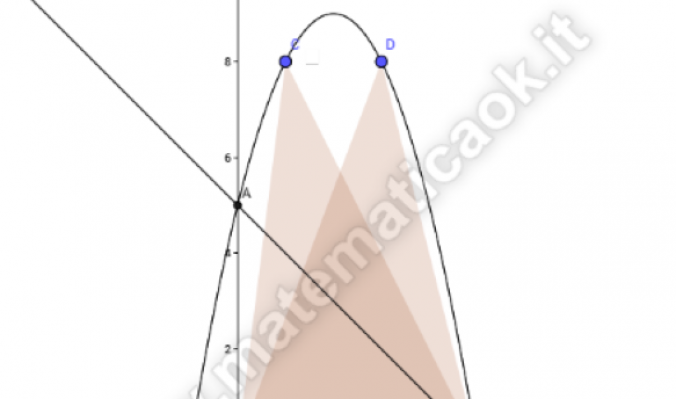
Esercizio 17 – Parabola e retta
Data la parabola di equazione y = — x2 + 4x + 5, determina: a) le intersezioni della parabola con la retta di equazione y = — x + 5 e indicale con A e B (A punto di ascissa minima); b) un punto P sull’arco di parabola AB in modo che il triangolo OPB abbia area 20.
Esercizio 16 – Fascio di parabole
a) Determiniamo liquazione del fascio di parabole con asse parallelo all’asse)’, passanti per i punti A (-1;0) e B( 1;2). b) Determiniamo l’equazione del fascio di parabole con asse parallelo all’asse y, tangenti nel punto T di ascissa 3 alla retta t di equazione y = 2x – 1.
Esercizio 15 – Fascio di parabole
Studia il fascio di parabole di equazione y = (3k — 2) x2 + 2 (3 — 5k) x — 4 + 7k e determina per quale valore di k la parabola del fascio: a) passa per il punto P(2; — 3); b) ha il vertice sull’asse y.
Esercizio 14 – Fascio di parabole
Nel fascio di parabole definito dalle parabole di equazioni y = x2 — 2x + 1 e y = — x2 + 4x + 1, determinare: a) l’equazione delle parabole degeneri; b) l’equazione della parabola passante per il punto P( —1; —2).
Esercizio 13 – Fascio di parabole
Studiamo il fascio di parabole rappresentato dall’equazione y = —(k + 2)x2 — x + k — 1, con k appartenente ad R.
Esercizio 13 – Fascio di parabole
Dato il fascio di parabole di equazione y = (k + 1) x2 — 3kx — 4, determina: a) le coordinate dei punti base; b) la parabola del fascio avente fuoco di ascissa 3; c) la parabola del fascio passante per P(—1; 1); d) le parabole del fascio tangenti alla retta di equazione y = 2x — 5.
Esercizio 12 – Parabola con parametro
Data la parabola di equazione y = x2 + 3x + 2k — 1, determina per quale valore di k essa risulta tangente alla retta passante per i punti A( —1; —4) e B(1; —1).