Esercizio 23 – Fascio di parabole
Esercizio 22 – Fascio di parabole
Esercizio 21 – Fascio di parabole
Esercizio 20 – Fascio di parabole
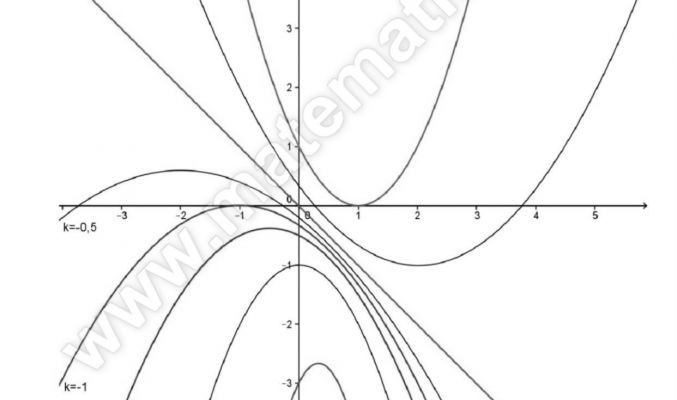
Dopo aver rappresentato le parabole di equazioni x = 2y2 — 4y e x = 3y2 + 4, scrivi l’equazione del fascio da esse individuato, infine determina le parabole degeneri.
Esercizio 19 – Fascio di parabole
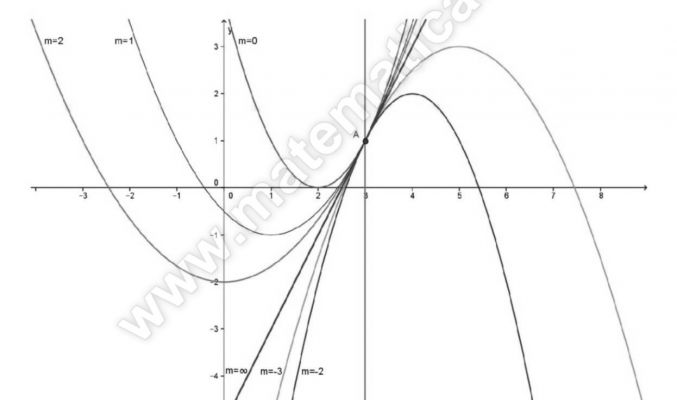
Considera il fascio di parabole di equazione (m + 1) y2 + (m — 1) x + 2(m — 1) y = 0 e studia le sue principali caratteristiche. Determina poi la parabola del fascio: a) passante per il punto P(2; — 2); b) tangente alla retta x – 2y – 2 = 0; c) che intercetta sul semiasse positivo delle ordinate un segmento di lunghezza 2.
Esercizio 59 – Trapezio isoscele – richiesto online da Pasquale
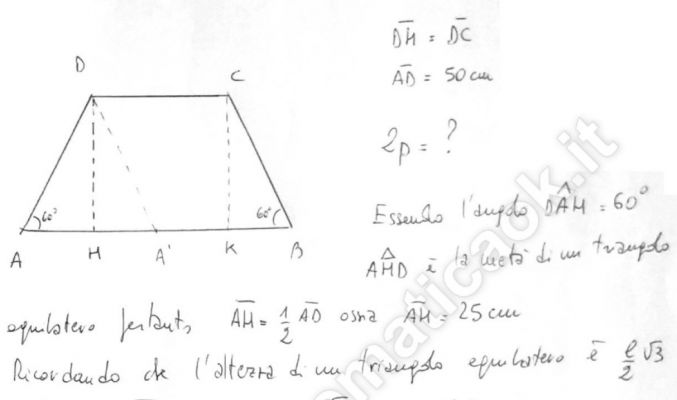
Gli angoli adiacente alla base maggiore di un trapezio isoscele misurano 60° ciascuno. Sapendo che l’altezza e la base minore sono fra loro congruenti e che il lato obliquo misura 50 cm, calcola il perimetro del trapezio.
Esercizio 58 – Trapezio rettangolo – richiesto online da Pasquale
In un trapezio rettangolo la base minore e il lato obliquo misurano 32 cm e 40 cm. Sapendo che l’angolo acuto adiacente alla base maggiore misurano 60°, calcola perimetro e area del trapezio.
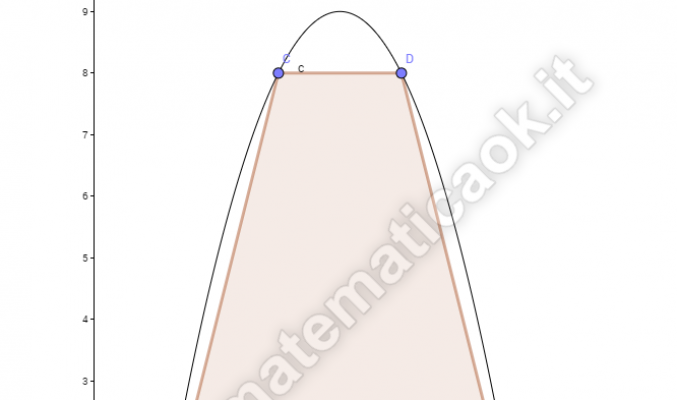
Esercizio 18 – Parabola e trapezio isoscele
Nella parte di piano definita dalla parabola di equazione y = — x2 + 8x — 7 e dall’asse x inscrivi un trapezio isoscele ABCD con la base maggiore AB sull’asse x. Trova le coordinate di C e D in modo che il trapezio abbia area 32.
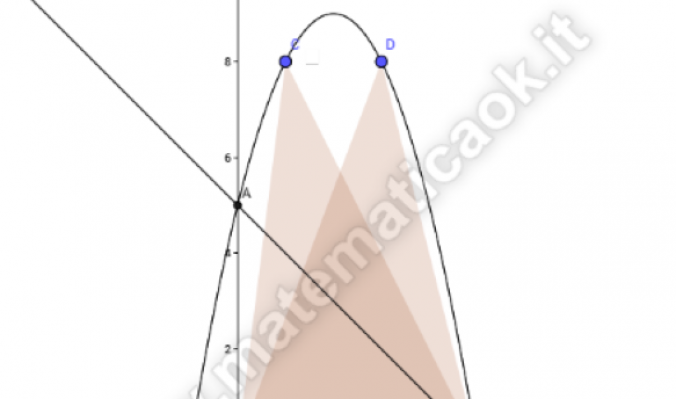
Esercizio 17 – Parabola e retta
Data la parabola di equazione y = — x2 + 4x + 5, determina: a) le intersezioni della parabola con la retta di equazione y = — x + 5 e indicale con A e B (A punto di ascissa minima); b) un punto P sull’arco di parabola AB in modo che il triangolo OPB abbia area 20.