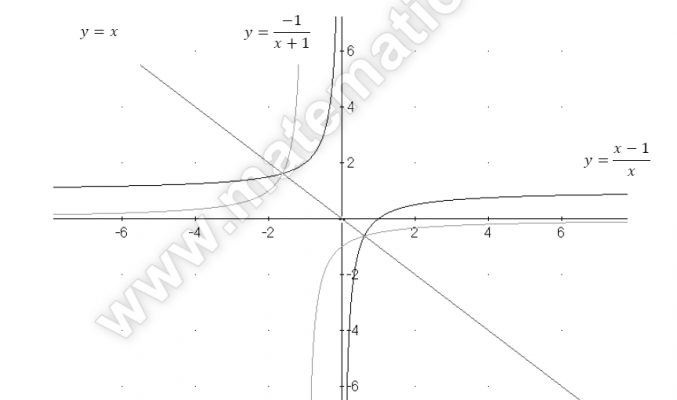
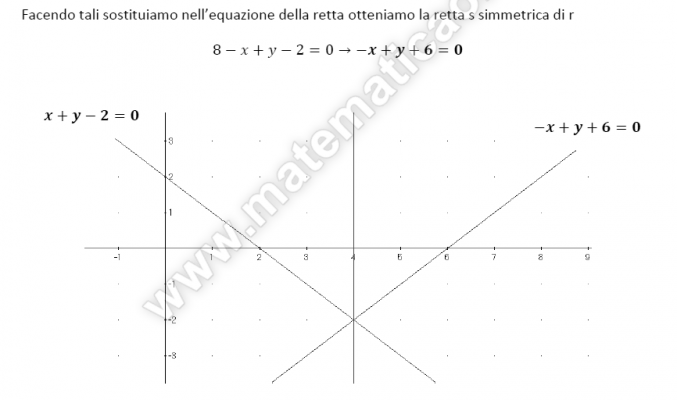
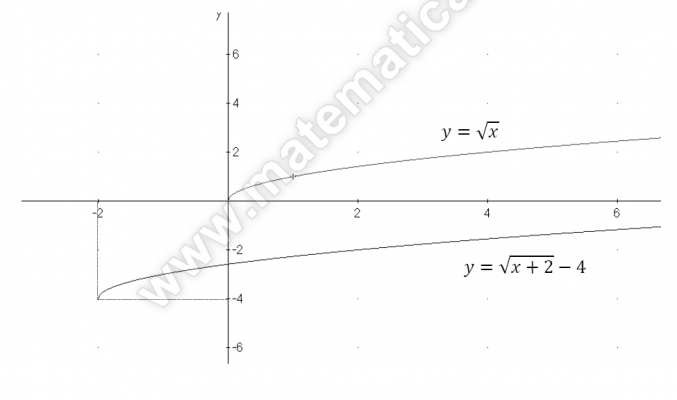
Esercizio 6 – Simmetria
Esercizio 5 – Simmetria
Esercizio 4 – Traslazione
Esercizio 3 – Traslazione
Esercizio 1 – Sistema simmetrico – richiesto online da Guglielmo
Formule di Waring
Alcune volte un sistema simmetrico potrebbe non presentarsi nella sua forma canonica ed in questi casi la risoluzione è più complicata. Esistono però delle formule che ci permettono di portare il sistema alla forma canonica e di risolverlo chiamate Formule di Waring:
Sistemi simmetrici
Un sistema in due incognite si dice simmetrico se è formato da equazioni simmetriche ossia equazioni che rimangono invariate scambiando tra loro le due incognite. Per poter risolvere un sistema simmetrico dobbiamo fare vari passaggi per portarlo in una forma particolare detta forma canonica del sistema: una volta portato il sistema in forma canonica le sue soluzioni sono: Quando il sistema si trova in forma canonica possiamo ricondurre il problema alla ricerca di…
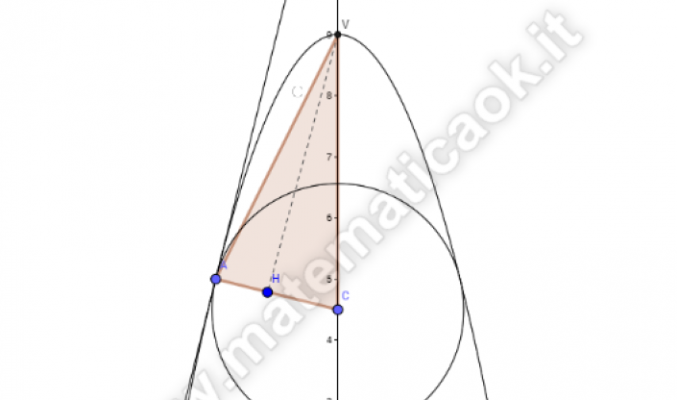
Esercizio 25 – Parabola, retta tangente e circonferenza
Determina e rappresenta l’equazione della parabola con asse parallelo all’asse y con vertice in V(0; 9) e passante per A ( — 2; 5). Successivamente trova e rappresenta l’equazione della retta t tangente in A alla parabola. Scrivi l’equazione della circonferenza con il centro C sull’asse y e tangente in A alla retta t e rappresentala graficamente. Detto V il vertice della parabola, calcola l’area del triangolo A VC.
Esercizio 24 – Fascio di parabole
Studia il fascio di parabole di equazione (m + 1) x2 — 4 (m + 1) x — (m + 1) y + 4 + 5m = 0 e determinare poi la parabola del fascio: a) passante per il punto A(3; — 3); b) che intercetta sull’asse delle ascisse un segmento di lunghezza 6; c) tangente alla retta 2x — y — 3 = 0; d) che forma nel I…