Il fiore colorato è delimitato da archi di circonferenza tracciati nel quadrato di lato 10 cm. Calcola l’area del fiore.
geometria piana
Esercizio 18 – Quadrato e porzione di corona circolare
Nel quadrato qui a lato, il cui perimetro misura 48 cm, puntando il compasso in D si tracciano due archi di raggio pari al lato e a metà lato. Calcola l’area della superficie colorata.
Esercizio 17 – Quadrato e semicerchi
Esercizio 16 – Triangolo e cerchio
Un triangolo equilatero che ha il lato di 30 cm è inscritto in una circonferenza. Trovare l’area del triangolo e l’area dei tre segmenti circolari delimitati dai lati del triangolo.
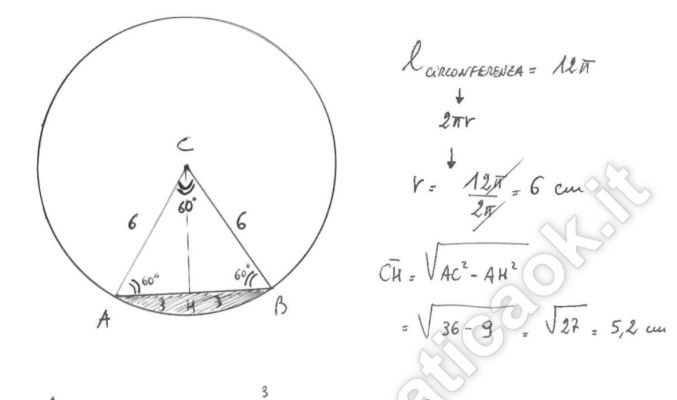
Esercizio 15 – Segmento circolare
Determina l’area del segmento circolare di base AB, sapendo che sull’arco AB, che limita il segmento, insiste un angolo al centro ACB di 60° e che la circonferenza misura 12 cm.
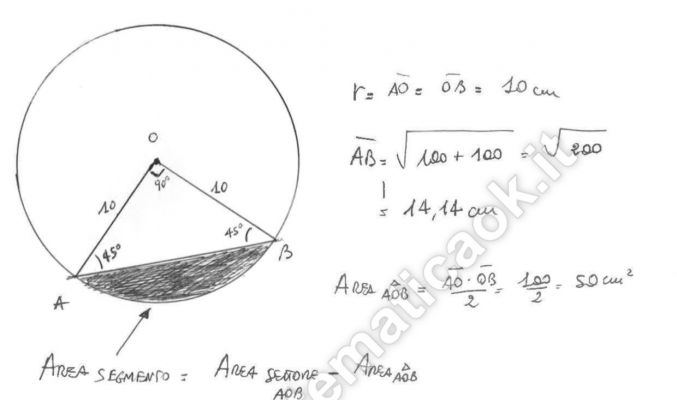
Esercizio 14 – Segmento circolare
Una circonferenza ha il raggio di 10 cm. Calcola l’area del segmento circolare che corrisponde a un angolo al centro di 90°.
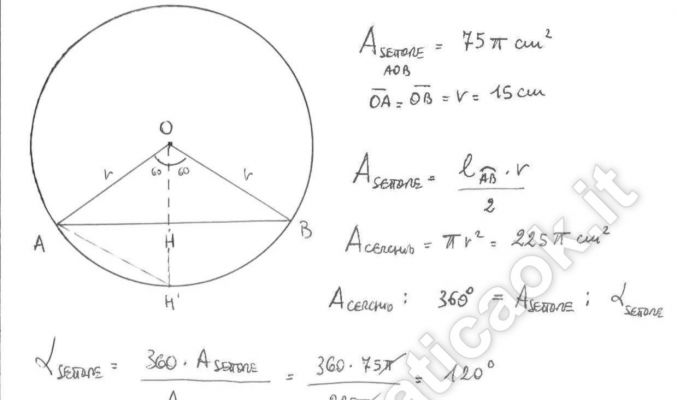
Esercizio 13 – Triangolo e circonferenza
Il triangolo AOB ha il vertice O nel centro della circonferenza e il lato AB è una corda che insiste sull’arco AB. Sapendo che il settore circolare AOB ha l’area di 75 cm2 e il raggio di 1 5 cm, calcola area e perimetro del triangolo.
Raggio del cerchio inscritto in un triangolo rettangolo
Inscrivibilità in una semicirconferenza
Un triangolo rettangolo si può sempre inscrivere in una semicirconferenza; ne consegue che la mediana relativa all’ipotenusa è la metà dell’ipotenusa ed è il raggio del cerchio circoscritto.
Secondo Teorema di Euclide
In un triangolo rettangolo, il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha per dimensioni le proiezioni dei cateti sull’ipotenusa. Ovvero CH2 = AH . HB