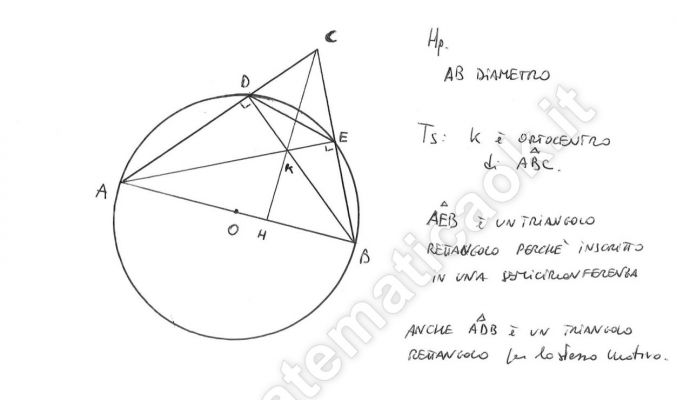
Considera il triangolo ABC con il lato AB coincidente con un diametro di una circonferenza e il vertice C esterno ad essa. Detti D ed E i punti di intersezione della circonferenza con i lati AC e BC, dimostrare che il punto di incontro delle diagonali del quadrilatero inscritto ABED coincide con l’ortocentro del triangolo ABC.
triangolo qualsiasi
Esercizio 39 – Triangolo ottusangolo – dimostrazione
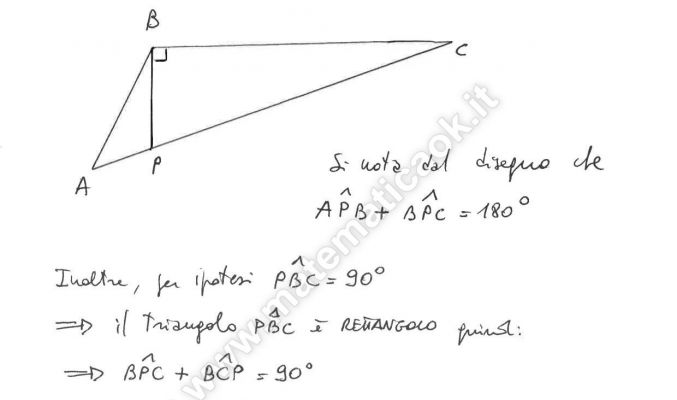
Nel triangolo ABC, ottusangolo in B, la perpendicolare in B a BC interseca AC nel punto P. Dimostrare che l’angolo APB è il supplementare del complementare dell’angolo in C.
Esercizio 38 – Triangoli qualsiasi – dimostrazione
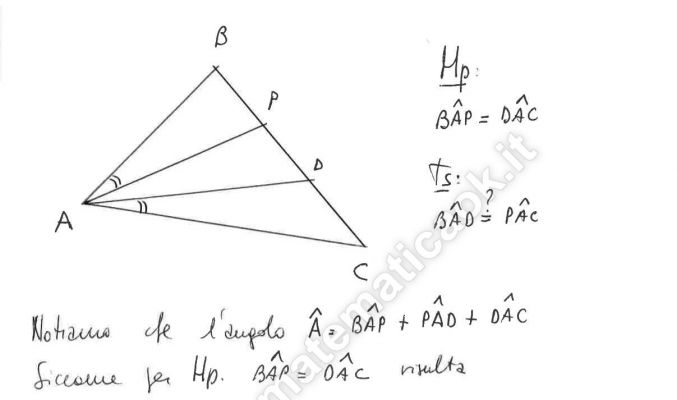
In un triangolo ABC il punto P del lato BC ed il punto D del segmento PC sono tali che BÂP = DÂC. Dimostrare che BÂD = PÂC.
Esercizio 36 – Triangolo e circonferenza inscritta
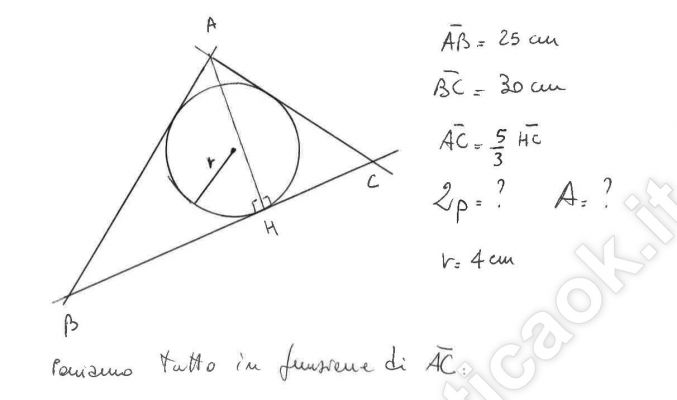
Nel triangolo ABC i lati AB e BC misurano rispettivamente 25 cm e 30 cm, il lato AC è uguale ai 5/3 della sua proiezione su BC. Determinare il perimetro e l’area del triangolo sapendo che il raggio della circonferenza in esso inscritta è 4 cm.
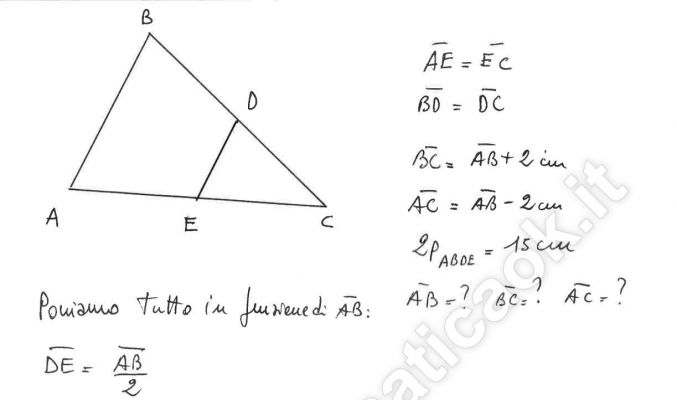
Esercizio 35 – Triangolo e trapezio
In un triangolo ABC, sia D il punto medio di BC ed E il punto medio di AC . Sapendo che il lato BC è 2 cm in più di AB; il lato AC è 2 cm in meno di AB e che il perimetro del trapezio ABDE è 15 cm, determina le lunghezze dei lati del triangolo.
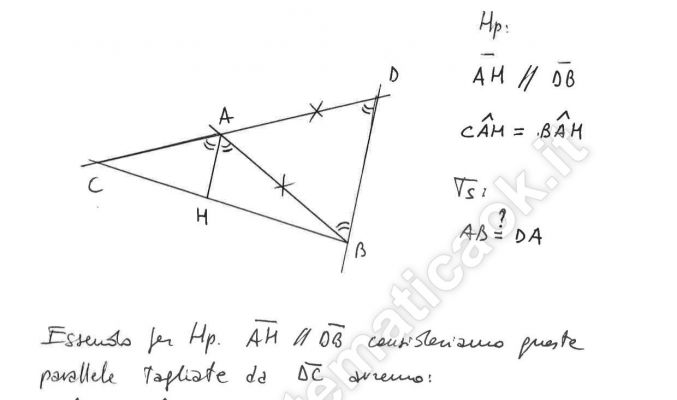
Esercizio 34 – Triangoli qualsiasi – Dimostrazione
Dato il triangolo ABC, condurre dal vertice B la parallela alla bisettrice dell’angolo in A e sia D il punto in cui tale parallela interseca il prolungamento del lato AC. Dimostrare che è AB=DA.
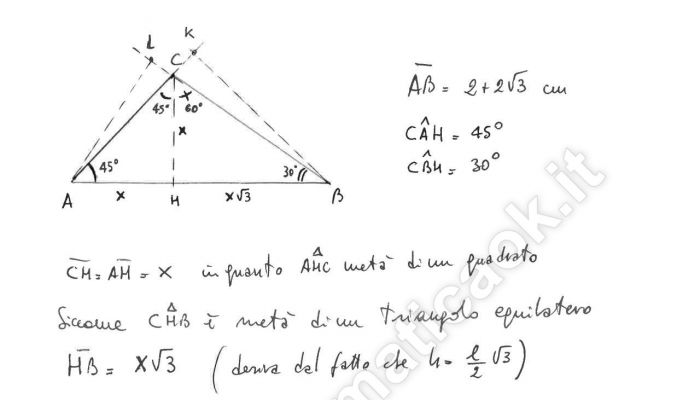
Esercizio 33 – Triangolo qualsiasi
La base di un triangolo è (2+2√3) cm, trovare l’altezza relativa agli altri due lati sapendo che gli angoli alla base sono di 45° e 30° (Suggerimento: si indichi con x l’altezza).
Come si calcola il raggio di una circonferenza inscritta in un triangolo qualsiasi
Per calcolare il raggio della circonferenza inscritta in un triangolo qualsiasi occorre conoscere il perimetro e l’area del triangolo. r = 2 × AREA / PERIMETRO r = AREA / semi PERIMETRO
Terzo criterio di similitudine tra triangoli
Secondo criterio di similitudine tra triangoli
Due triangoli sono simili se: due lati del primo triangolo sono proporzionali ad altri due lati del secondo, con lo stesso rapporto; l’angolo compreso tra i due lati del primo triangolo è congruente all’angolo compreso tra i due lati dell’altro triangolo.