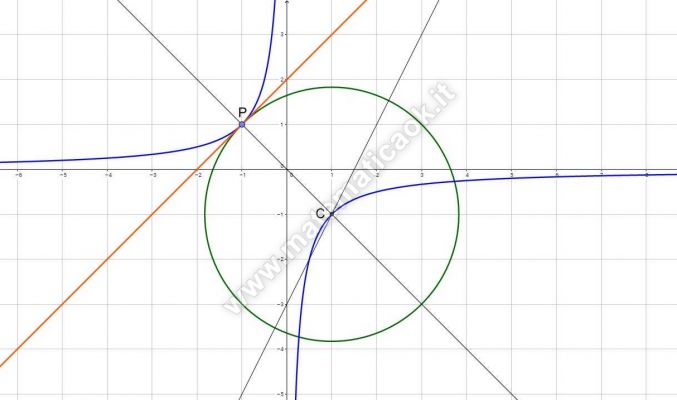
Scrivere l’equazione della circonferenza tangente alla retta y=x+2 nel punto P(-l;l) ed avente centro sulla retta di equazione 2x-y-3=0. Determinare poi l’equazione dell’iperbole equilatera riferita ai propri asintoti che passa per il centro della circonferenza.
circonferenza
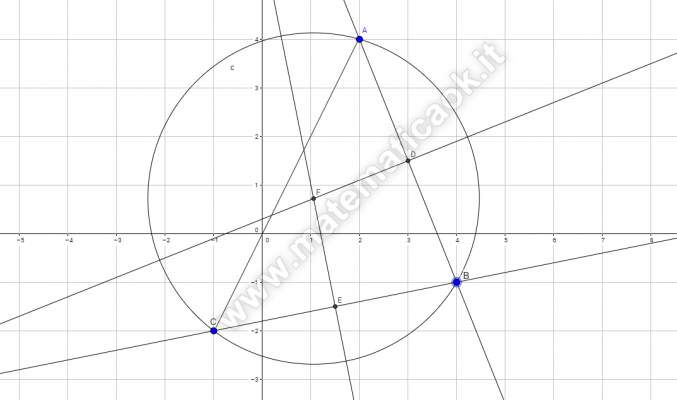
Esercizio 27 – Trovare il Circocentro – richiesto online da Paolo
Determina il centro della circonferenza circoscritta al triangolo di vertici A(2;4), B(4; -1), C(-1;-2).
Esercizio 26 – Circonferenza e rette
Scrivi l’equazione della retta parallela all’asse x sulla quale la circonferenza di equazione x2 + y2 + 2x + 8y = 0 stacca una corda di lunghezza 4√2
Esercizio 25 – Fascio di circonferenze
Considera il fascio di circonferenze di equazione x2 + y2 + (2 – k) x + (k – 8) y – 3 + k = 0 e studia le sue caratteristiche. Trova per quali valori di k si ha la circonferenza: a) passante per l’origine; b) di raggio uguale a ; c) tangente all’asse y; d) con il centro che ha distanza dall’origine minore di 5/2 .
Esercizio 24 – Fascio di circonferenze
Studia le caratteristiche del fascio di circonferenze di equazione x2 + y2 — 2(k — 3)x + ky— 6k + 14 = 0. a) Stabilisci per quali valori di k l’equazione rappresenta una circonferenza. b) Determina per quali valori di k si hanno le circonferenze del fascio che incontrano l’asse delle y in due punti A e B tali che AB = √56.
Esercizio 23 – Circonferenze e rette
Determinare se la retta 2x – y + 1 = 0 è TANGENTE, SECANTE o ESTERNA alla circonferenza di equazione x2 + y2– 2x + 4y = 0
Esercizio 22 – Intersezione di circonferenze
Calcolare la lunghezza della corda comune alle seguenti circonferenze: x2 + y2 – 4x + 8y = 0 e x2 + y2 + 2x – 10y – 24 = 0
Esercizio 21 – Circonferenze e rette
Scrivere l’equazione della circonferenza passante per l’origine O ed avente il centro nel punto comune alle rette: 3x – y + 7 = 0 e x – y + 1 = 0
Esercizio 20 – Circonferenze e punti
Determinare se il punto A(1,-2) è interno, esterno o appartiene alla circonferenza di equazione x2 + y2 -8x -4y -5 = 0
Esercizio 19 – Fascio di circonferenze
Studia il fascio di circonferenze di equazione x2 + y2 – (2 + k) x + (k – 2) y + 2 = 0 indicando le sue caratteristiche. Trova poi la circonferenza del fascio: a) tangente all’asse x; b) che racchiude un’area 8; c) il cui centro appartiene alla retta y = 2x – 5; d) tangente alla retta y = x – 4.